题目内容
【题目】已知定义在
上的函数
满足
，且
，则下列说法正确的有（ ）
（1）若函数
，则函数
是奇函数；
（2）
；
（3）设函数
，则函数
的图象经过点
；
（4）设
，若数列
是等比数列，则
.
A.（2）（3）（4）B.（1）（3）（4）C.（1）（3）D.（1）（2）（3）（4）
【答案】B
【解析】
根据奇函数定义可判断（1）；根据表达式并结合赋值法，即可判断（2）（3）；由所给表达式，分别求得
与
，检验两个是否相等，由等比中项判断数列
是否为等比数列，即可判断（4）.
对于（1），
，所以函数
是奇函数，故（1）正确；
对于（2），令
，
，代入可得
，因为
，
；
令，
，则
，
，故（2）错误；
对于（3），令，
，则
，
，即函数
的图象经过点
，故（3）正确；
对于（4），令，
，则
，，
，
；
当
，由
可知
所以
，
，
∵数列
是等比数列，
，
即
，
故（4）正确，
故选:B.
【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况，对该公司2018年连续六个月的利润进行了统计，并根据得到的数据绘制了相应的折线图，如图所示
（1）由折线图可以看出，可用线性回归模型拟合月利润
（单位：百万元）与月份代码
之间的关系，求关于的线性回归方程，并预测该公司2019年3月份的利润；
（2）甲公司新研制了一款产品，需要采购一批新型材料，现有
，
两种型号的新型材料可供选择，按规定每种新型材料最多可使用
个月，但新材料的不稳定性会导致材料损坏的年限不相同，现对，两种型号的新型材料对应的产品各
件进行科学模拟测试，得到两种新型材料使用寿命的频数统计如下表：
使用寿命 材料类型 |
|
|
|
| 总计 |
|
|
|
|
|
|
|
|
|
|
|
|
如果你是甲公司的负责人，你会选择采购哪款新型材料？
参考数据：
，
.参考公式：回归直线方程为
，其中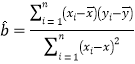
.
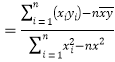【题目】某大型歌手选秀活动，过程分为初赛、复赛和决赛.经初赛进入复赛的40名选手被平均分成甲、乙两个班，由组委会聘请两位导师各负责一个班进行声乐培训.下图是根据这40名选手参加复赛时获得的100名大众评审的支持票数制成的茎叶图.赛制规定：参加复赛的40名选手中，获得的支持票数不低于85票的可进入决赛，其中票数不低于95票的选手在决赛时拥有“优先挑战权”.
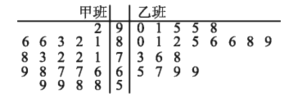
（1）从进入决赛的选手中随机抽出2名，X表示其中拥有“优先挑战权”的人数，求X的分布列和数学期望；
（2）请填写下面的
列联表，并判断能否在犯错误的概率不超过0.025的前提下认为进入决赛与选择的导师有关？
甲班 | 乙班 | 合计 | |
进入决赛 | |||
未进入决赛 | |||
合计 |
下面的临界值表仅供参考：
P（ | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：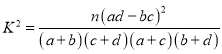
，其中
）
