题目内容
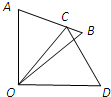 如图,△COD是△AOB绕点O顺时针旋转36°后得到的图形,点C恰好在AB上,∠AOD的度数是90°,则∠B的度数是
如图,△COD是△AOB绕点O顺时针旋转36°后得到的图形,点C恰好在AB上,∠AOD的度数是90°,则∠B的度数是考点:相似三角形的性质
专题:选作题,几何证明
分析:已知△COD是△AOB绕点O顺时针方向旋转36°后所得的图形,可得△COD≌△AOB,旋转角为36°,根据点C恰好在AB上,则△AOC为等腰三角形,可结合三角形的内角和定理求∠B的度数.
解答:解:根据旋转性质得△COD≌△AOB,
∴CO=AO,
由旋转角为36°,可得∠AOC=∠BOD=36°,
∴∠OAC=(180°-∠AOC)÷2=72°,
∠BOC=∠AOD-∠AOC-∠BOD=18°,
∠AOB=∠AOC+∠BOC=54°,
在△AOB中,由内角和定理得∠B=180°-∠OAC-∠AOB=180°-72°-54°=54°.
故答案为:54°.
∴CO=AO,
由旋转角为36°,可得∠AOC=∠BOD=36°,
∴∠OAC=(180°-∠AOC)÷2=72°,
∠BOC=∠AOD-∠AOC-∠BOD=18°,
∠AOB=∠AOC+∠BOC=54°,
在△AOB中,由内角和定理得∠B=180°-∠OAC-∠AOB=180°-72°-54°=54°.
故答案为:54°.
点评:本题考查旋转的性质.旋转变化前后,对应角分别相等,同时要充分运用内角和定理求角.

练习册系列答案
相关题目
已知函数f(x)=ex-ax-b,若f(x)≥0恒成立,则ab的最大值为( )
A、
| ||
| B、e2 | ||
| C、e | ||
D、
|
已知A(-4,2,3)关于xOz平面的对称点为A1,A1关于z轴的对称点为A2,则|AA2|等于( )
| A、8 | B、12 | C、16 | D、19 |
设n∈N*,若(
-1)n=x+
y(x,y∈Z),则x的值( )
| 2 |
| 2 |
| A、一定是偶数 |
| B、一定是奇数 |
| C、与n的奇偶性相同 |
| D、与n的奇偶性相反 |
 如图,D、E分别是AB、AC上两点,CD与BE相交于点O,下列条件中不能使△ABE和△ACD相似的是( )
如图,D、E分别是AB、AC上两点,CD与BE相交于点O,下列条件中不能使△ABE和△ACD相似的是( )| A、∠B=∠C | B、∠ADC=∠AEB | C、BE=CD,AB=AC | D、AD:AC=AE:AB |
圆内接四边形ABCD中,cosA+cosB+cosC+cosD等于( )
| A、0 | B、4 | C、2 | D、不确定 |
已知f(x)是定义在R上的函数,且对任意实数x有f(x+4)=-f(x)+2
,若函数y=f(x-1)的图象关于直线x=1对称,则f(2014)=( )
| 2 |
A、-2+2
| ||
B、2+2
| ||
C、2
| ||
D、
|
 如图,AB是圆O的直径,C,D是圆O上两点,AC与BD相交于点E,GC,GD是圆O的切线,点F在DG的延长线上,且DG=GF.求证:
如图,AB是圆O的直径,C,D是圆O上两点,AC与BD相交于点E,GC,GD是圆O的切线,点F在DG的延长线上,且DG=GF.求证: