题目内容
 如图,AB是圆O的直径,C,D是圆O上两点,AC与BD相交于点E,GC,GD是圆O的切线,点F在DG的延长线上,且DG=GF.求证:
如图,AB是圆O的直径,C,D是圆O上两点,AC与BD相交于点E,GC,GD是圆O的切线,点F在DG的延长线上,且DG=GF.求证:(1)D、E、C、F四点共圆;
(2)GE⊥AB.
考点:圆內接多边形的性质与判定,圆的切线的性质定理的证明
专题:几何证明
分析:(1)如图,连接OC,OD,则OC⊥CG,OD⊥DG,可得四点O,D,G,C共圆.设∠CAB=∠1,∠DBA=∠2,∠ACO=∠3,可得∠COB=2∠1,∠DOA=2∠2.于是∠DGC=180°-∠DOC=2(∠1+∠2).利用切线长定理可得DG=CG,而DG=GF,可得GF=GC.从而可得∠F=∠1+∠2.可得∠DEC+∠F=180°,即可证明.
(2)延长GE交AB于H.由GD=GC=GF,可得点G是经过D,E,C,F四点的圆的圆心.可得GE=GC,∠GCE=∠GEC.又∠GCE+∠3=90°,∠1=∠3,可得∠AEH+∠1=90°,进而得出证明.
(2)延长GE交AB于H.由GD=GC=GF,可得点G是经过D,E,C,F四点的圆的圆心.可得GE=GC,∠GCE=∠GEC.又∠GCE+∠3=90°,∠1=∠3,可得∠AEH+∠1=90°,进而得出证明.
解答: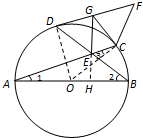 解:(1)如图,连接OC,OD,则OC⊥CG,OD⊥DG,
解:(1)如图,连接OC,OD,则OC⊥CG,OD⊥DG,
∴四点O,D,G,C共圆.
设∠CAB=∠1,∠DBA=∠2,∠ACO=∠3,
∠COB=2∠1,∠DOA=2∠2.
∴∠DGC=180°-∠DOC=2(∠1+∠2).
∵DG=GF,DG=CG.
∴GF=GC.
∴∠GCF=∠F.
∵∠DGC=2∠F,
∴∠F=∠1+∠2.
又∵∠DEC=∠AEB=180°-(∠1+∠2),
∴∠DEC+∠F=180°,
∴D,E,C,F四点共圆.
(2)延长GE交AB于H.
∵GD=GC=GF,
∴点G是经过D,E,C,F四点的圆的圆心.
∴GE=GC,
∴∠GCE=∠GEC.
又∵∠GCE+∠3=90°,∠1=∠3,
∴∠GEC+∠3=90°,
∴∠AEH+∠1=90°,
∴∠EHA=90°,
即GE⊥AB.
 解:(1)如图,连接OC,OD,则OC⊥CG,OD⊥DG,
解:(1)如图,连接OC,OD,则OC⊥CG,OD⊥DG,∴四点O,D,G,C共圆.
设∠CAB=∠1,∠DBA=∠2,∠ACO=∠3,
∠COB=2∠1,∠DOA=2∠2.
∴∠DGC=180°-∠DOC=2(∠1+∠2).
∵DG=GF,DG=CG.
∴GF=GC.
∴∠GCF=∠F.
∵∠DGC=2∠F,
∴∠F=∠1+∠2.
又∵∠DEC=∠AEB=180°-(∠1+∠2),
∴∠DEC+∠F=180°,
∴D,E,C,F四点共圆.
(2)延长GE交AB于H.
∵GD=GC=GF,
∴点G是经过D,E,C,F四点的圆的圆心.
∴GE=GC,
∴∠GCE=∠GEC.
又∵∠GCE+∠3=90°,∠1=∠3,
∴∠GEC+∠3=90°,
∴∠AEH+∠1=90°,
∴∠EHA=90°,
即GE⊥AB.
点评:本题综合考查了四点共圆的判定与性质、切线长定理、圆的切线的性质、互余角之间的关系、垂直的判定等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在航天员进行的一项太空实验中,先后要实施6个程序,其中程序B和C都不与D相邻,则实验顺序的编排方法共有( )
| A、216种 | B、288种 | C、180种 | D、144种 |
下列四边形中,四个顶点一定在同一个圆上的是( )
| A、平行四边行 | B、菱形 | C、矩形 | D、直角梯形 |
下列那些点既在曲线C1:
(0≤θ<π,θ为参数)又在曲线 C2:
(t∈R,t为参数)上( )
|
|
A、(1,
| ||||
B、(-1,±
| ||||
C、(1,
| ||||
D、(1,±
|
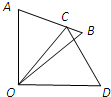 如图,△COD是△AOB绕点O顺时针旋转36°后得到的图形,点C恰好在AB上,∠AOD的度数是90°,则∠B的度数是
如图,△COD是△AOB绕点O顺时针旋转36°后得到的图形,点C恰好在AB上,∠AOD的度数是90°,则∠B的度数是 ”为:
”为: ,运算“
,运算“ ”为:
”为: ,设
,设 ,若
,若
 ( )
( )