题目内容
圆内接四边形ABCD中，cosA+cosB+cosC+cosD等于（ ）
| A、0 | B、4 | C、2 | D、不确定 |
考点：圆內接多边形的性质与判定
专题：直线与圆
分析：根据圆内接四边形的性质，得A+C=B+D=180°，结合诱导公式得到cosB与cosD互为相反数，且cosA与cosC互为相反数，由此能求出结果．
解答：解：∵四边形ABCD为圆内接四边形
∴A+C=B+D=180°，
∴cosB=-cosD，cosA=-cosC，
可得cosA+cosB+cosC+cosD
=（cosA+cosC）+（cosB+cosD）=0
故选：A．
∴A+C=B+D=180°，
∴cosB=-cosD，cosA=-cosC，
可得cosA+cosB+cosC+cosD
=（cosA+cosC）+（cosB+cosD）=0
故选：A．
点评：本题求圆内接四边形的四个内角的余弦之和．着重考查了圆内接四边形的性质、三角函数的诱导公式等知识，属于基础题．
练习册系列答案
相关题目
依据表
下列选项中，哪一个样本所得的k值没有充分的证据显示“X与Y有关系”（ ）
| P（K2≥k） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A、k=6.665 |
| B、k=3.765 |
| C、k=2.710 |
| D、k=2.700 |
使得（3x2+
）n（n∈N+）的展开式中含有常数项的最小的n=（ ）
| 2 |
| x3 |
| A、3 | B、5 | C、6 | D、10 |
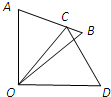如图，△COD是△AOB绕点O顺时针旋转36°后得到的图形，点C恰好在AB上，∠AOD的度数是90°，则∠B的度数是
如图，AB为⊙O的弦，C是弧AB的中点，过点B作直线BD，连接CD交AB于点N，若∠CDB=30°，则∠CNB=在极坐标系中，过点（2，
）且垂直于极轴的直线的极坐标方程是（ ）
| π |
| 6 |
A、ρ=
| ||
B、ρ=
| ||
C、ρsinθ=
| ||
D、ρcosθ=
|