题目内容
设n∈N*,若(
-1)n=x+
y(x,y∈Z),则x的值( )
| 2 |
| 2 |
| A、一定是偶数 |
| B、一定是奇数 |
| C、与n的奇偶性相同 |
| D、与n的奇偶性相反 |
考点:二项式系数的性质
专题:二项式定理
分析:利用二项式定理把等式的左边展开,求得x的解析式,可得x的值的情况.
解答:解:∵(
-1)n=x+
y(x,y∈Z),
(
-1)n=
•(
)n-
•(
)n-1+
•(
)n-2+…+
•
•(-1)n-1+
•(-1)n,
故x=(-1)n+(-1)n-2
(
)2+(-1)n-4
(
)4+…=2M±1,(其中,M为整数).
故答案为:B.
| 2 |
| 2 |
(
| 2 |
| C | 0 n |
| 2 |
| C | 1 n |
| 2 |
| C | 2 n |
| 2 |
| C | n-1 n |
| 2 |
| C | n n |
故x=(-1)n+(-1)n-2
| C | 2 n |
| 2 |
| C | 4 n |
| 2 |
故答案为:B.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
若复数z=sinθ-
+(cosθ-
)i(i是虚数单位)是纯虚数,则tanθ值为( )
| 3 |
| 5 |
| 4 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
在航天员进行的一项太空实验中,先后要实施6个程序,其中程序B和C都不与D相邻,则实验顺序的编排方法共有( )
| A、216种 | B、288种 | C、180种 | D、144种 |
使得(3x2+
)n(n∈N+)的展开式中含有常数项的最小的n=( )
| 2 |
| x3 |
| A、3 | B、5 | C、6 | D、10 |
 已知某篮球运动员2013年度参加了25场比赛,我从中抽取5场,用茎叶图统计该运动员5场中的得分如图所示,则该样本的方差为( )
已知某篮球运动员2013年度参加了25场比赛,我从中抽取5场,用茎叶图统计该运动员5场中的得分如图所示,则该样本的方差为( )| A、25 | B、24 | C、18 | D、16 |
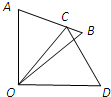 如图,△COD是△AOB绕点O顺时针旋转36°后得到的图形,点C恰好在AB上,∠AOD的度数是90°,则∠B的度数是
如图,△COD是△AOB绕点O顺时针旋转36°后得到的图形,点C恰好在AB上,∠AOD的度数是90°,则∠B的度数是