题目内容
已知矩阵M=
的两个特征值分别为λ1=-1和λ2=4,
(Ⅰ)求实数a,b的值;
(Ⅱ)若直线l在矩阵M所对应的线性变换作用下的象的方程为x-2y-3=0,求直线l的方程.
|
(Ⅰ)求实数a,b的值;
(Ⅱ)若直线l在矩阵M所对应的线性变换作用下的象的方程为x-2y-3=0,求直线l的方程.
考点:矩阵特征值的定义
专题:矩阵和变换
分析:(Ⅰ)根据矩阵M的两个特征值分别为λ1=-1和λ2=4,代入特征多项式,求出a、b的值即可;
(Ⅱ)确定变换前后坐标之间的关系,利用直线l′:x-2y-3=0,求出直线l的方程即可.
(Ⅱ)确定变换前后坐标之间的关系,利用直线l′:x-2y-3=0,求出直线l的方程即可.
解答:解:(Ⅰ)矩阵M的特征多项式f(λ)=
=(λ-2)(λ-b)-2a,
又∵矩阵M的两个特征值分别为λ1=-1和λ2=4,
∴f(-1)=0,f(4)=0,
∴
,
解得a=3,b=1;
(Ⅱ)设P(x,y)是直线l上任意一点,它在矩阵M对应的变换下变为点P′(x′,y′),
则
=
,
即
;
∵点P′(x′,y′)在直线l′:x-2y-3=0上,
∴x′-2y′-3=0,
把x′,y′代人得:2x-y+3=0.
故所求直线l的方程为:2x-y+3=0.
|
又∵矩阵M的两个特征值分别为λ1=-1和λ2=4,
∴f(-1)=0,f(4)=0,
∴
|
解得a=3,b=1;
(Ⅱ)设P(x,y)是直线l上任意一点,它在矩阵M对应的变换下变为点P′(x′,y′),
则
|
|
|
即
|
∵点P′(x′,y′)在直线l′:x-2y-3=0上,
∴x′-2y′-3=0,
把x′,y′代人得:2x-y+3=0.
故所求直线l的方程为:2x-y+3=0.
点评:本题主要考查了特征值与特征向量的计算,考查了矩阵变换的运用,属于基础题.

练习册系列答案
相关题目
若复数z=sinθ-
+(cosθ-
)i(i是虚数单位)是纯虚数,则tanθ值为( )
| 3 |
| 5 |
| 4 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
在极坐标系中,过点(2,
)且垂直于极轴的直线的极坐标方程是( )
| π |
| 6 |
A、ρ=
| ||
B、ρ=
| ||
C、ρsinθ=
| ||
D、ρcosθ=
|
下列那些点既在曲线C1:
(0≤θ<π,θ为参数)又在曲线 C2:
(t∈R,t为参数)上( )
|
|
A、(1,
| ||||
B、(-1,±
| ||||
C、(1,
| ||||
D、(1,±
|
 已知某篮球运动员2013年度参加了25场比赛,我从中抽取5场,用茎叶图统计该运动员5场中的得分如图所示,则该样本的方差为( )
已知某篮球运动员2013年度参加了25场比赛,我从中抽取5场,用茎叶图统计该运动员5场中的得分如图所示,则该样本的方差为( )| A、25 | B、24 | C、18 | D、16 |
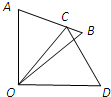 如图,△COD是△AOB绕点O顺时针旋转36°后得到的图形,点C恰好在AB上,∠AOD的度数是90°,则∠B的度数是
如图,△COD是△AOB绕点O顺时针旋转36°后得到的图形,点C恰好在AB上,∠AOD的度数是90°,则∠B的度数是 ,
, ,若
,若 ,则
,则 的值为( )
的值为( )
