题目内容
已知函数 .
.
(1)若 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)若函数 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围;
(3)设函数 ,若在
,若在 上至少存在一点
上至少存在一点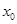 ,使得
,使得 >
> 成立,求实数
成立,求实数 的取值范围.
的取值范围.
 .
.(1)若
 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;(2)若函数
 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围;(3)设函数
 ,若在
,若在 上至少存在一点
上至少存在一点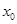 ,使得
,使得 >
> 成立,求实数
成立,求实数 的取值范围.
的取值范围.(1) ;(2)实数
;(2)实数 的取值范围是
的取值范围是 ;(3)实数
;(3)实数 的取值范围
的取值范围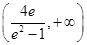 .
.
 ;(2)实数
;(2)实数 的取值范围是
的取值范围是 ;(3)实数
;(3)实数 的取值范围
的取值范围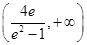 .
.试题分析:(1)求
 的导数,找出
的导数,找出 处的导数即切线的斜率,由点斜式列出直线的方程即可;(2)求出函数的定义域,在定义域内利用导数与函数增减性的关系,转化为恒成立问题进行求解即可;(3)讨论
处的导数即切线的斜率,由点斜式列出直线的方程即可;(2)求出函数的定义域,在定义域内利用导数与函数增减性的关系,转化为恒成立问题进行求解即可;(3)讨论 在定义域上的最值,分情况讨论
在定义域上的最值,分情况讨论 的增减性,进而解决
的增减性,进而解决 存在成立的问题即可.
存在成立的问题即可.(1)当
 时,函数
时,函数 ,
,
 ,曲线
,曲线 在点
在点 处的切线的斜率为
处的切线的斜率为
从而曲线
 在点
在点 处的切线方程为
处的切线方程为 ,即
,即 3分
3分(2)
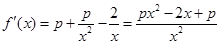
令
 ,要使
,要使 在定义域
在定义域 内是增函数,只需
内是增函数,只需 在
在 内恒成立
内恒成立由题意
 ,
, 的图象为开口向上的抛物线,对称轴方程为
的图象为开口向上的抛物线,对称轴方程为
∴
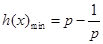 , 只需
, 只需 ,即
,即 时,
时,
∴
 在
在 内为增函数,正实数
内为增函数,正实数 的取值范围是
的取值范围是 7分
7分(3)∵
 在
在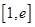 上是减函数
上是减函数∴
 时,
时, ;
;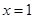 时,
时, ,即
,即
①当
 时,
时, ,其图象为开口向下的抛物线,对称轴
,其图象为开口向下的抛物线,对称轴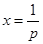 在
在 轴的左侧,且
轴的左侧,且 ,所以
,所以 在
在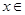
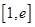 内是减函数
内是减函数当
 时,
时, ,因为
,因为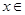
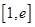 ,所以
,所以 ,
,
此时,
 在
在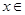
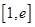 内是减函数
内是减函数故当
 时,
时, 在
在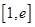 上单调递减
上单调递减 ,不合题意
,不合题意②当
 时,由
时,由 ,所以
,所以
又由(Ⅱ)知当
 时,
时, 在
在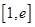 上是增函数
上是增函数∴
 ,不合题意 12分
,不合题意 12分③当
 时,由(Ⅱ)知
时,由(Ⅱ)知 在
在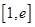 上是增函数,
上是增函数,
又
 在
在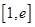 上是减函数,故只需
上是减函数,故只需 ,
,
而
 ,
,
即
 ,解得
,解得
所以实数
 的取值范围是
的取值范围是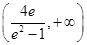 15分.
15分.
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为


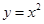 在点
在点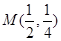 处的切线的倾斜角是 ( )
处的切线的倾斜角是 ( )
 ,和抛物线相切且与直线
,和抛物线相切且与直线 平行的的直线方程为 ( )
平行的的直线方程为 ( )
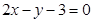



 在点(1,1)处的切线方程 。
在点(1,1)处的切线方程 。 ,则a=( )
,则a=( )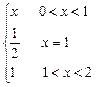 则f(x)的连续区间为( )
则f(x)的连续区间为( )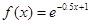 在x=4处的导数
在x=4处的导数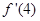 = .
= .