Question

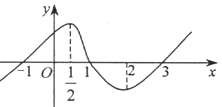
【题目】如图，在直三棱柱A1B1C1﹣ABC中，AB=AC=AA1 ， ，点D是BC的中点．
（I）求证：AD⊥平面BCC1B1；
（II）求证：A1B∥平面ADC1；
（III）求二面角A﹣A1B﹣D的余弦值．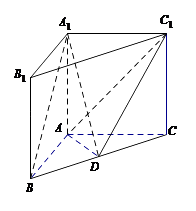

Answer 1

【答案】解：（I）因AB=AC，D为BC中点，故AD⊥BC 又因在直三棱柱A1B1C1﹣ABC中，CC1⊥平面ABC，故AD⊥CC1
又BC∩CC1=C，
故AD⊥平面BCC1B1
用向量方法证明本题请对应给分．
本题可分别以AB，AC，AA1为x，y，z轴建立空间直角坐标系，
也可分别以DC，DA，AD1（D1为棱B1C1中点）为x，y，z轴建立空间直角坐标系．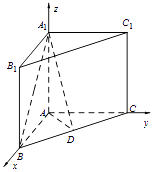

（II）如图，连接A1C∩AC1=E，连接DE．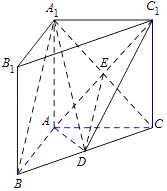

因D、E分别是BC、A1C的中点，故DE是△A1BC的中位线
故A1B∥DE（6分）．因A1B平面ADC1
故A1B∥平面ADC1 ．
用向量方法证明本题请如下给分：求出平面ADC1的法向量，
因A1B平面ADC1 ，
故A1B∥平面ADC1
（III）解法一：连接B1A∩BA1=O，分别取OB、AB中点H、O1 ， 连接DH、DO1 ．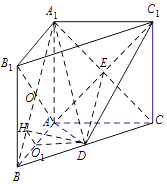

因为四边形ABB1A1是正方形且O1 ， H分别是BA，BO中点，故HO1⊥AB．
又因O1 ， H分别是BA，BC中点且AB⊥AC，故O1D⊥AB，
故∠O1HD就是二面角A﹣A1B﹣D的平面角．
设AB=2，则在Rt△HO1D中，∠HO1D=90°且 ，
故 ，故 ．
解法二：设AB=AC=2，则 ，故AB2+AC2=BC2 ， 故AB⊥AC，
又因三棱柱A1B1C1﹣ABC为直三棱柱，故AB，AC，AA1两两垂直，故可建系如图．
则平面AA1B的法向量为 ．
又 ，
设平面A1BD的法向量 ，
则 ．
令z=1可得
设所求二面角为θ，由图可知θ为锐角，故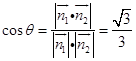
【解析】（Ⅰ）根据线面垂直的判定定理进行证明即可，（Ⅱ）根据线面平行的判定定理进行证明即可．（III）根据二面角的定义或者建立空间坐标系，求出平面的法向量，利用向量法进行求解即可．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行，以及对直线与平面垂直的判定的理解，了解一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．