题目内容
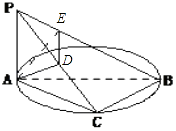
【题目】平面α内有一以AB为直径的圆,PA⊥α,点C在圆周上移动(不与A,B重合),点D,E分别是A在PC,PB上的射影,则( )
A.∠ACD是二面角A﹣PC﹣B的平面角
B.∠AED是二面角A﹣PB﹣C的平面角
C.∠EDA是二面角A﹣PC﹣B的平面角
D.∠DAE是二面角B﹣PA﹣C的平面角
【答案】B
【解析】解:∵PA⊥⊙O所在平面α,BCα,
∴PA⊥BC,
∵AB是⊙O的直径,
∴BC⊥AC,
∵PA∩AC=A,
∴BC⊥平面PAC,
∴AD⊥BC,
又∵D是点A在PC上的射影,
∴AD⊥PC,
∵BC∩PC=C,
∴AD⊥平面PBC,
∴AD⊥PB,
又∵AE⊥PB,AD∩AE=A
∴PB⊥面ADE,
∴∠AED是二面角A﹣PB﹣C的平面角.
所以答案是:B.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目