题目内容
【题目】某学校为了加强学生数学核心素养的培养，锻炼学生自主探究学习的能力，他们以教材第97页B组第3题的函数
为基本素材，研究该函数的相关性质，取得部分研究成果如下：
①同学甲发现：函数
是偶函数；
②同学乙发现：对于任意的
都有
；
③同学丙发现：对于任意的
，都有
；
④同学丁发现：对于函数定义域中任意的两个不同实数
，总满足
.
其中所有正确研究成果的序号是__________．
【答案】②③.
【解析】
①利用奇偶函数的定义判断；
②只需要计算等式两端验证即可；
③只需要计算等式两端验证即可；
④根据复合函数单调性判断
单调性即可．
解：①定义域
关于原点对称，
，是奇函数，①错误；
②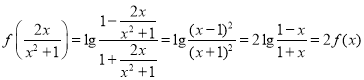
，②正确；
③由于
，
且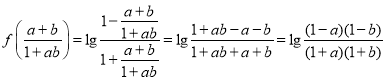
，则③正确；
④
，由于
单调递减，
单调递增，所以单调递减，
，④错误；
故答案为②③．
【题目】在某超市，随机调查了100名顾客购物时使用手机支付的情况，得到如下的
列联表，已知其中从使用手机支付的人群中随机抽取1人，抽到青年的概率为
.
（1）根据已知条件完成列联表，并根据此资料判断是否有
的把握认为“超市购物用手机支付与年龄有关”？
（2）现采用分层抽样从这100名顾客中按照“使用手机支付”和“不使用手机支付”中抽取得到一个容量为5的样本，设事件
为“从这个样本中任选3人，这3人中至少有2人是使用手机支付的”，求事件发生的概率？
列联表
青年 | 中老年 | 合计 | |
使用手机支付 | 60 | ||
不使用手机支付 | 28 | ||
合计 | 100 |
|
|
|
|
| 0.001 |
|
|
|
|
| 10.828 |
附：
【题目】某校在本校任选了一个班级，对全班50名学生进行了作业量的调查，根据调查结果统计后，得到如下的
列联表，已知在这50人中随机抽取2人，这2人都“认为作业量大”的概率为
.
认为作业量大 | 认为作业量不大 | 合计 | |
男生 | 18 | ||
女生 | 17 | ||
合计 | 50 |
（1）请完成上面的列联表；
（2）根据列联表的数据，能否有
的把握认为“认为作业量大”与“性别”有关？
附表：
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
附：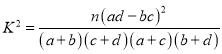
（其中
）
