题目内容
【题目】如图,在圆内接四边形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
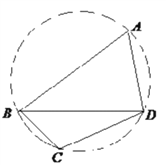
(1)求![]() 的大小;
的大小;
(2)求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:
(1)在![]() 中,由余弦定理得
中,由余弦定理得![]() ,则
,则![]() ,结合圆的内接四边形的性质可得
,结合圆的内接四边形的性质可得![]() .
.
(2)法1:在![]() 中,由余弦定理得
中,由余弦定理得![]() ,结合均值不等式的结论有
,结合均值不等式的结论有![]() ,则
,则![]() .
.![]()
![]() .当且仅当
.当且仅当![]() ,
,![]() 面积的最大值为
面积的最大值为![]() .
.
法2:由几何关系可知,当![]() 为弧
为弧![]() 中点时,
中点时,![]() 上的高最大,此时
上的高最大,此时![]() 是等腰三角形,此时
是等腰三角形,此时![]() 上的高
上的高![]() ,据此可得
,据此可得![]() 面积的最大值为
面积的最大值为![]() .
.
试题解析:
(1)在![]() 中,由余弦定理得
中,由余弦定理得
![]()
![]() ,
,
解得![]() ,
,
注意到![]() ,
,
可得![]() .
.
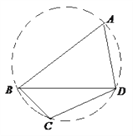
(2)法1:在![]() 中,由余弦定理得
中,由余弦定理得
![]() ,
,
即![]()
![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() .
.
∴![]()
![]()
![]() .
.
当且仅当![]() ,△BCD为等腰三角形时等号成立,
,△BCD为等腰三角形时等号成立,
即![]() 面积的最大值为
面积的最大值为![]() .
.
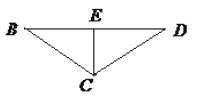
法2:如图,当![]() 为弧
为弧![]() 中点时,
中点时,![]() 上的高最大,此时
上的高最大,此时![]() 是等腰三角形,易得
是等腰三角形,易得![]() ,作
,作![]() 上的高
上的高![]() ,
,
在![]() 中,由
中,由![]() ,
,![]() ,得
,得![]() ,
,
可得![]()
![]() ,
,
综上知,即![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目