题目内容
已知函数f(x)=ln x,g(x)=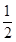 x2-bx(b为常数).
x2-bx(b为常数).
(1)函数f(x)的图像在点(1,f(1))处的切线与g(x)的图像相切,求实数b的值;
(2)设h(x)=f(x)+g(x),若函数h(x)在定义域上存在单调减区间,求实数b的取值范围;
(3)若b>1,对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,求实数b的取值范围.
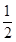 x2-bx(b为常数).
x2-bx(b为常数).(1)函数f(x)的图像在点(1,f(1))处的切线与g(x)的图像相切,求实数b的值;
(2)设h(x)=f(x)+g(x),若函数h(x)在定义域上存在单调减区间,求实数b的取值范围;
(3)若b>1,对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,求实数b的取值范围.
(1)-1±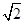
(2)(2,+∞)
(3)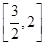
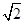
(2)(2,+∞)
(3)
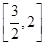
解:(1)因为f(x)=ln x,所以f′(x)=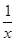 ,因此f′(1)=1,所以函数f(x)的图像在点(1,f(1))处的切线方程为y=x-1.
,因此f′(1)=1,所以函数f(x)的图像在点(1,f(1))处的切线方程为y=x-1.
由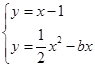
消去y,得x2-2(b+1)x+2=0.
所以Δ=4(b+1)2-8=0,
解得b=-1±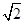 .
.
(2)因为h(x)=f(x)+g(x)
=ln x+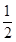 x2-bx(x>0),
x2-bx(x>0),
所以h′(x)=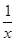 +x-b=
+x-b=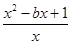 .
.
由题意知,h′(x)<0在(0,+∞)上有解.
因为x>0,设u(x)=x2-bx+1,
则u(0)=1>0,
所以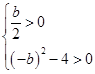 ,解得b>2.
,解得b>2.
所以实数b的取值范围是(2,+∞).
(3)不妨设x1>x2.
因为函数f(x)=ln x在区间[1,2]上是增函数,所以f(x1)>f(x2),函数g(x)图像的对称轴为直线x=b,且b>1.
(ⅰ)当b≥2时,函数g(x)在区间[1,2]上是减函数,所以g(x1)<g(x2),所以|f(x1)-f(x2)|>|g(x1)-g(x2)|等价于f(x1)-f(x2)>g(x2)-g(x1),即f(x1)+g(x1)>f(x2)+g(x2),等价于h(x)=f(x)+g(x)=ln x+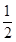 x2-bx(x>0)在区间[1,2]上是增函数,即等价于h′(x)=
x2-bx(x>0)在区间[1,2]上是增函数,即等价于h′(x)=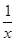 +x-b≥0在区间[1,2]上恒成立,亦等价于b≤x+
+x-b≥0在区间[1,2]上恒成立,亦等价于b≤x+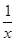 在区间[1,2]上恒成立,所以b≤2.
在区间[1,2]上恒成立,所以b≤2.
又b≥2,所以b=2;
(ⅱ)当1<b<2时,函数g(x)在区间[1,b]上是减函数,在[b,2]上为增函数.
①当1≤x2<x1≤b时,|f(x1)-f(x2)|>|g(x1)-g(x2)|等价于f(x1)-f(x2)>g(x2)-g(x1),等价于f(x1)+g(x1)>f(x2)+g(x2),等价于h(x)=f(x)+g(x)=ln x+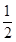 x2-bx(x>0)在区间[1,b]上是增函数,等价于h′(x)=
x2-bx(x>0)在区间[1,b]上是增函数,等价于h′(x)=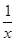 +x-b≥0在区间[1,b]上恒成立,等价于b≤x+
+x-b≥0在区间[1,b]上恒成立,等价于b≤x+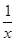 在区间[1,b]上恒成立,所以b≤2.
在区间[1,b]上恒成立,所以b≤2.
又1<b<2,所以1<b<2;
②当b≤x2<x1≤2时,|f(x1)-f(x2)|>|g(x1)-g(x2)|等价于f(x1)-f(x2)>g(x1)-g(x2)等价于f(x1)-g(x1)>f(x2)-g(x2),等价于H(x)=f(x)-g(x)=ln x-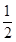 x2+bx在区间[b,2]上是增函数,等价于H′(x)=
x2+bx在区间[b,2]上是增函数,等价于H′(x)=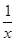 -x+b≥0在区间[b,2]上恒成立,等价于b≥x-
-x+b≥0在区间[b,2]上恒成立,等价于b≥x-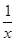 在区间[b,2]上恒成立,所以b≥
在区间[b,2]上恒成立,所以b≥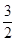 ,故
,故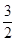 ≤b<2;
≤b<2;
③当1≤x2<b<x1≤2时,由g(x)图像的对称性知,只要|f(x1)-f(x2)|>|g(x1)-g(x2)|对于①②同时成立,那么对于③,
则存在t1∈[1,b],使|f(x1)-f(x2)|>|f(t1)-f(x2)|>|g(t1)-g(x2)|=|g(x1)-g(x2)|恒成立;
或存在t2∈[b,2],使|f(x1)-f(x2)|>
|f(x1)-f(t2)|>|g(x1)-g(t2)|=
|g(x1)-g(x2)|恒成立.
因此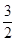 ≤b<2.
≤b<2.
综上所述,实数b的取值范围是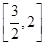 .
.
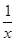 ,因此f′(1)=1,所以函数f(x)的图像在点(1,f(1))处的切线方程为y=x-1.
,因此f′(1)=1,所以函数f(x)的图像在点(1,f(1))处的切线方程为y=x-1.由
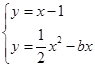
消去y,得x2-2(b+1)x+2=0.
所以Δ=4(b+1)2-8=0,
解得b=-1±
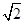 .
.(2)因为h(x)=f(x)+g(x)
=ln x+
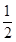 x2-bx(x>0),
x2-bx(x>0),所以h′(x)=
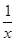 +x-b=
+x-b=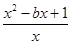 .
.由题意知,h′(x)<0在(0,+∞)上有解.
因为x>0,设u(x)=x2-bx+1,
则u(0)=1>0,
所以
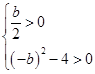 ,解得b>2.
,解得b>2.所以实数b的取值范围是(2,+∞).
(3)不妨设x1>x2.
因为函数f(x)=ln x在区间[1,2]上是增函数,所以f(x1)>f(x2),函数g(x)图像的对称轴为直线x=b,且b>1.
(ⅰ)当b≥2时,函数g(x)在区间[1,2]上是减函数,所以g(x1)<g(x2),所以|f(x1)-f(x2)|>|g(x1)-g(x2)|等价于f(x1)-f(x2)>g(x2)-g(x1),即f(x1)+g(x1)>f(x2)+g(x2),等价于h(x)=f(x)+g(x)=ln x+
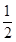 x2-bx(x>0)在区间[1,2]上是增函数,即等价于h′(x)=
x2-bx(x>0)在区间[1,2]上是增函数,即等价于h′(x)=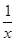 +x-b≥0在区间[1,2]上恒成立,亦等价于b≤x+
+x-b≥0在区间[1,2]上恒成立,亦等价于b≤x+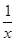 在区间[1,2]上恒成立,所以b≤2.
在区间[1,2]上恒成立,所以b≤2.又b≥2,所以b=2;
(ⅱ)当1<b<2时,函数g(x)在区间[1,b]上是减函数,在[b,2]上为增函数.
①当1≤x2<x1≤b时,|f(x1)-f(x2)|>|g(x1)-g(x2)|等价于f(x1)-f(x2)>g(x2)-g(x1),等价于f(x1)+g(x1)>f(x2)+g(x2),等价于h(x)=f(x)+g(x)=ln x+
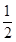 x2-bx(x>0)在区间[1,b]上是增函数,等价于h′(x)=
x2-bx(x>0)在区间[1,b]上是增函数,等价于h′(x)=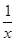 +x-b≥0在区间[1,b]上恒成立,等价于b≤x+
+x-b≥0在区间[1,b]上恒成立,等价于b≤x+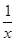 在区间[1,b]上恒成立,所以b≤2.
在区间[1,b]上恒成立,所以b≤2.又1<b<2,所以1<b<2;
②当b≤x2<x1≤2时,|f(x1)-f(x2)|>|g(x1)-g(x2)|等价于f(x1)-f(x2)>g(x1)-g(x2)等价于f(x1)-g(x1)>f(x2)-g(x2),等价于H(x)=f(x)-g(x)=ln x-
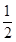 x2+bx在区间[b,2]上是增函数,等价于H′(x)=
x2+bx在区间[b,2]上是增函数,等价于H′(x)=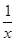 -x+b≥0在区间[b,2]上恒成立,等价于b≥x-
-x+b≥0在区间[b,2]上恒成立,等价于b≥x-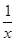 在区间[b,2]上恒成立,所以b≥
在区间[b,2]上恒成立,所以b≥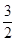 ,故
,故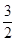 ≤b<2;
≤b<2;③当1≤x2<b<x1≤2时,由g(x)图像的对称性知,只要|f(x1)-f(x2)|>|g(x1)-g(x2)|对于①②同时成立,那么对于③,
则存在t1∈[1,b],使|f(x1)-f(x2)|>|f(t1)-f(x2)|>|g(t1)-g(x2)|=|g(x1)-g(x2)|恒成立;
或存在t2∈[b,2],使|f(x1)-f(x2)|>
|f(x1)-f(t2)|>|g(x1)-g(t2)|=
|g(x1)-g(x2)|恒成立.
因此
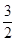 ≤b<2.
≤b<2.综上所述,实数b的取值范围是
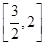 .
.
练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 ,其中
,其中 且
且 .
. 在点
在点 处的切线与
处的切线与 上有且仅有一个极值点,求实数
上有且仅有一个极值点,求实数 的取值范围.
的取值范围.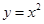 在点
在点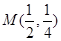 处的切线的倾斜角是 ( )
处的切线的倾斜角是 ( )

 在点(1,1)处的切线方程 。
在点(1,1)处的切线方程 。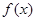 与
与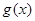 都是定义在R上的函数,
都是定义在R上的函数,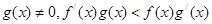 ,且
,且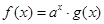
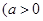 ,且
,且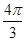 ,在有穷数列
,在有穷数列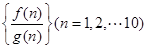 中,任意取前
中,任意取前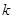 项相加,则前
项相加,则前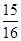 的概率是( )
的概率是( )


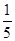
 在点
在点 处的切线方程为 .
处的切线方程为 . ,则a=( )
,则a=( )