题目内容
已知等比数列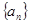 的公比为
的公比为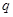 ,
,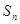 是
是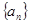 的前
的前 项和.
项和.
(1)若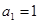 ,
,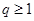 ,求
,求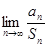 的值;
的值;
(2)若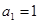 ,
,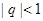 ,
,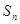 有无最值?并说明理由;
有无最值?并说明理由;
(3)设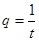 ,若首项
,若首项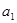 和
和 都是正整数,
都是正整数, 满足不等式:
满足不等式: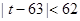 ,且对于任意正整数
,且对于任意正整数 有
有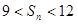 成立,问:这样的数列
成立,问:这样的数列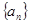 有几个?
有几个?
(1) ;(2)
;(2)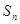 有最大值为
有最大值为 ,最小值为
,最小值为 ;(3)
;(3) 个.
个.
解析试题分析:(1)根据等比数列前 项和公式
项和公式 ,可见要对
,可见要对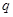 分类讨论,当
分类讨论,当 时,
时, ,
, ,
, ,从而不难求出
,从而不难求出 ;当
;当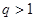 时,
时,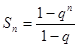 ,
, ,
, ,即可利用根据定义求出
,即可利用根据定义求出 ;(2)根据题意可求出数列的前
;(2)根据题意可求出数列的前 项和
项和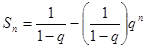 ,要求出
,要求出 的最值,可见要分
的最值,可见要分 和
和 两种情况进行讨论,当
两种情况进行讨论,当 时利用单调性即可求出
时利用单调性即可求出 的最值情况,当
的最值情况,当 时,由于
时,由于 将随着
将随着 的奇偶性正负相间,故又要再次以
的奇偶性正负相间,故又要再次以 的奇偶数进行讨论,再利用各自的单调性即可求出
的奇偶数进行讨论,再利用各自的单调性即可求出 的最值; (3)首先由含有
的最值; (3)首先由含有 的绝对值不等式可求出
的绝对值不等式可求出 的范围,再用
的范围,再用 表示出
表示出 ,由单调性不难求出
,由单调性不难求出 的最小值
的最小值 ,即
,即 ,故
,故 并分别代入进行,依据
并分别代入进行,依据 就可求出
就可求出 的范围,最后结合
的范围,最后结合 是正整数,从而确定出
是正整数,从而确定出 的个数.
的个数.
试题解析:(1)当 时,
时, ,
, ,
, 2分
2分
当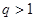 时,
时,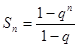 ,
, ,
, 4分
4分
所以 (可以写成
(可以写成 ;
;
(2)若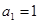 ,
,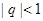 ,则
,则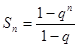 ,
,
当 时,
时,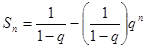 ,所以
,所以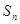 随
随 的增大而增大,
的增大而增大,
而 ,此时
,此时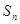 有最小值为1,但无最大值. 6分
有最小值为1,但无最大值. 6分
当 时,
时,
①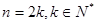 时,
时, ,所以
,所以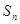 随
随 的增大而增大,
的增大而增大,
即 是偶数时,
是偶数时, ,即:
,即: ; 8分
; 8分
②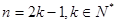 时,
时, ,
,
即: ,所以
,所以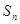 随
随 的增大而减小,
的增大而减小,
即 是奇数时,
是奇数时, ,即:
,即: ;
;
由①②得:

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
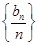 为等比数列,并求数列{bn}的通项公式.
为等比数列,并求数列{bn}的通项公式.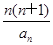 ,求实数λ的最大值.
,求实数λ的最大值.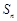 是等比数列
是等比数列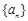 的前
的前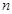 项和,
项和,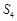 、
、 、
、 成等差数列,且
成等差数列,且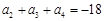 .
.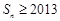 ?若存在,求出符合条件的所有
?若存在,求出符合条件的所有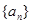 的前
的前 项和
项和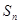 ,已知
,已知 ,
,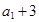 ,
,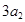 ,
,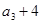 成等差数列.
成等差数列.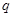 和通项
和通项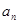 ;
;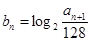 ,求
,求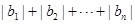 .
.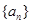 是公比大于1的等比数列,
是公比大于1的等比数列,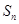 为数列
为数列 项和.已知
项和.已知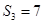 ,且
,且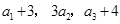 构成等差数列.
构成等差数列.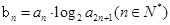 ,求数列
,求数列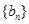 的前n项和
的前n项和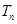 .
.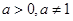 ,数列
,数列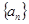 是首项为
是首项为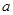 ,公比也为
,公比也为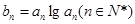
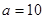 ,求数列
,求数列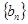 的前
的前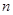 项和
项和 ;
;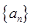 的前
的前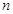 项和为
项和为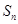 ,数列
,数列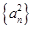 的前
的前 ,且
,且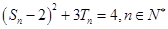 .
. 对
对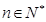 恒成立,求
恒成立,求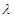 的最小值;
的最小值;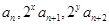 成等差数列,求正整数
成等差数列,求正整数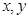 的值.
的值.