题目内容
已知数列{an}满足:a1=1,a2=2,2an=an-1+an+1(n≥2,n∈N*),数列{bn}满足b1=2,anbn+1=2an+1bn.
(1)求数列{an}的通项an;
(2)求证:数列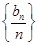 为等比数列,并求数列{bn}的通项公式.
为等比数列,并求数列{bn}的通项公式.
(1) an= n (2) bn=n·2n
解析解:(1)∵2an=an-1+an+1,∴数列{an}为等差数列.
又a1=1,a2=2,所以d=a2-a1=2-1=1,
数列{an}的通项an=a1+(n-1)d=1+(n-1)×1=n.
(2)∵an=n,∴nbn+1=2(n+1)bn,∴ =2·
=2·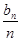 ,
,
所以数列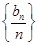 是以
是以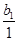 =2为首项,q=2为公比的等比数列,
=2为首项,q=2为公比的等比数列,
∴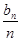 =2×2n-1,∴bn=n·2n.
=2×2n-1,∴bn=n·2n.

练习册系列答案
相关题目
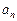 }的前n项和为
}的前n项和为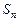 ,且
,且 .
.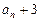 }为等比数列
}为等比数列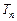
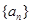 的前
的前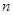 项和为
项和为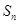 ,且
,且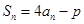 ,其中
,其中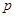 是不为零的常数.
是不为零的常数.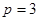 时,数列
时,数列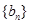 满足
满足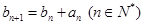 ,
,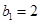 ,求数列
,求数列 的各项均满足
的各项均满足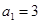 ,
, ,
,

 的通项公式是
的通项公式是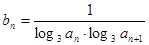 ,前
,前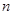 项和为
项和为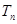 ,
,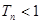 .
. bn=1.
bn=1.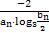 ,{cn}的前n项和为Tn,若Tn<
,{cn}的前n项和为Tn,若Tn<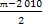 对一切n∈N*都成立,求最小正整数m.
对一切n∈N*都成立,求最小正整数m.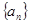 的公比为
的公比为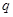 ,
,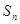 是
是 项和.
项和.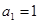 ,
,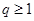 ,求
,求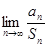 的值;
的值;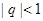 ,
,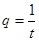 ,若首项
,若首项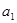 和
和 都是正整数,
都是正整数,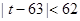 ,且对于任意正整数
,且对于任意正整数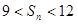 成立,问:这样的数列
成立,问:这样的数列 ,3
,3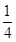 ,5
,5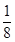 ,7
,7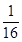 ,…
,…