Question

【题目】已知两个无穷数列分别满足，，

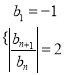其中，设数列的前项和分别为，

（1）若数列都为递增数列，求数列的通项公式；

（2）若数列满足：存在唯一的正整数（），使得，称数列为“坠点数列”

①若数列为“5坠点数列”，求；

②若数列为“坠点数列”，数列为“坠点数列”，是否存在正整数，使得，若存在，求的最大值；若不存在，说明理由.

Answer 1

【答案】（1），（2）①②

【解析】

(1)∵数列都为递增数列，

∴由递推式可得,，

则数列为等差数列,数列从第二项起构成等比数列．

∴；

(2)①∵数列满足：存在唯一的正整数k=5,使得,且，

∴数列必为1，3，5，7，5，7，9，11，…，即前4项为首项为1，公差为2的等差数列，从第5项开始为首项5，公差为2的等差数列，

故；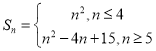

②∵，即，∴，而数列为“坠点数列”且，数列中有且只有两个负项.假设存在正整数，使得，显然，且为奇数，而中各项均为奇数，∴必为偶数. .

ⅰ.当时，，

当时，，故不存在，使得成立.

ⅱ.当时，，显然不存在，使得成立.

ⅲ.当时，，当时，才存在，使得成立.所以.当时，，构造为1,3,1,3,5,7,9，…，为-1,2,4,8，-16,32，…，此时，所以的最大值为6.