题目内容
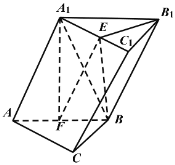
【题目】在边长为2的菱形![]() 中,
中,![]() ,将菱形
,将菱形![]() 沿对角线
沿对角线![]() 折起,使二面角
折起,使二面角![]() 的大小为
的大小为![]() ,则所得三棱锥
,则所得三棱锥![]() 的外接球表面积为( )
的外接球表面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
由已知可得![]() 、
、![]() 都是边长为
都是边长为![]() 的等边三角形,由菱形的对角线互相垂直,可得
的等边三角形,由菱形的对角线互相垂直,可得![]() 为二面角
为二面角![]() 的平面角,即
的平面角,即![]() ,作出图形,找出三棱锥
,作出图形,找出三棱锥![]() 的外接球球心,利用四点共圆结合正弦定理求解三棱锥
的外接球球心,利用四点共圆结合正弦定理求解三棱锥![]() 的外接球的半径,代入球的表面积公式可得结果.
的外接球的半径,代入球的表面积公式可得结果.
由于四边形![]() 是边长为
是边长为![]() 的菱形,且
的菱形,且![]() ,则
,则![]() ,
,
所以,![]() 、
、![]() 都是边长为
都是边长为![]() 的等边三角形,
的等边三角形,
由于菱形的对角线互相垂直,则![]() ,
,![]() ,
,
所以,![]() 为二面角
为二面角![]() 的平面角,即
的平面角,即![]() ,
,
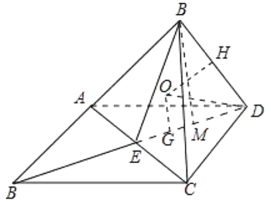
过点![]() 作平面
作平面![]() 的垂线
的垂线![]() ,垂足为点
,垂足为点![]() ,则点
,则点![]() 在线段
在线段![]() 上,
上,
由![]() ,
,![]() ,可得
,可得![]() ,
,
且![]() 是等边三角形,所以,
是等边三角形,所以,![]() ,
,
设![]() 的外心为点
的外心为点![]() ,
,![]() 的中点
的中点![]() ,
,
在平面![]() 内,过点
内,过点![]() 、
、![]() 分别作平面
分别作平面![]() 、
、![]() 的垂线交于点
的垂线交于点![]() ,
,
则点![]() 为三棱锥
为三棱锥![]() 的外接球的球心,则
的外接球的球心,则![]() ,
,![]() ,
,
![]() ,则
,则![]() ,
,
由于![]() 、
、![]() 、
、![]() 、
、![]() 四点共圆,可得
四点共圆,可得![]() ,
,
所以,三棱锥![]() 的外接球的表面积为
的外接球的表面积为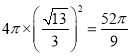 .
.
故选:B.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】新冠肺炎疫情这只“黑天鹅”的出现,给经济运行带来明显影响,住宿餐饮、文体娱乐、交通运输、旅游等行业受疫情影响严重.随着复工复产的有序推动,我市某西餐厅推出线上促销活动:
A套餐(在下列食品中6选3)
西式面点:蔓越莓核桃包、南瓜芝土包、黑列巴、全麦吐司;
中式面点:豆包、桂花糕
B套餐:酱牛肉、老味烧鸡熟食类组合.
复工复产后某一周两种套餐的日销售量(单位:份)如下:
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | |
A套餐 | 11 | 12 | 14 | 18 | 22 | 19 | 23 |
B套餐 | 6 | 13 | 15 | 15 | 37 | 20 | 41 |
(1)根据上面一周的销量,计算A套餐和B套餐的平均销量和方差,并根据所得数据评价两种套餐的销售情况;
(2)若某顾客购买一份A套餐,求他所选的面点中至少一种中式面点的概率.