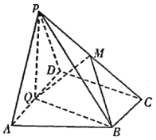
题目内容
【题目】已知三棱柱![]() 的侧棱和底面垂直,且所有顶点都在球O的表面上,侧面
的侧棱和底面垂直,且所有顶点都在球O的表面上,侧面![]() 的面积为
的面积为![]() .给出下列四个结论:
.给出下列四个结论:
①若![]() 的中点为E,则
的中点为E,则![]() 平面
平面![]() ;
;
②若三棱柱![]() 的体积为
的体积为![]() ,则
,则![]() 到平面
到平面![]() 的距离为3;
的距离为3;
③若![]() ,
,![]() ,则球O的表面积为
,则球O的表面积为![]() ;
;
④若![]() ,则球O体积的最小值为
,则球O体积的最小值为![]() .
.
当则所有正确结论的序号是( )
A.①④B.②③C.①②③D.①③④
【答案】D
【解析】
①,证明![]() ,
,![]() 平面
平面![]() 即得证,所以该命题正确;
即得证,所以该命题正确;
②,求出![]() 到平面
到平面![]() 的距离为2,所以该命题错误;
的距离为2,所以该命题错误;
③,求出![]() ,即可判断该命题正确;
,即可判断该命题正确;
④,求出外接球的半径的最小值为2,即得球O体积的最小值为![]() ,所以该命题正确.
,所以该命题正确.
①,如图,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .因为
.因为![]() ,所以
,所以![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,所以该命题正确;
,所以该命题正确;
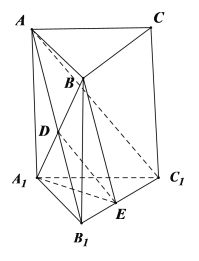
②,连接![]() ,过
,过![]() 作
作![]() ,垂足为
,垂足为![]() ,因为平面
,因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() 到平面
到平面![]() 的距离就是
的距离就是![]() .由题得
.由题得![]()
![]()
![]() ,所以
,所以![]() ,所以
,所以![]() 到平面
到平面![]() 的距离为2.所以该命题不正确;
的距离为2.所以该命题不正确;
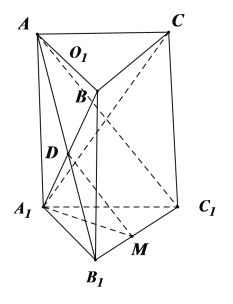
③,如图,取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() 的中点就是三棱柱的外接球的球心
的中点就是三棱柱的外接球的球心![]() ,连接
,连接![]() .设
.设![]() ,球的半径为
,球的半径为![]() ,则
,则![]() 所以
所以![]() .由题得
.由题得![]() ,所以
,所以![]() .所以
.所以![]() ,所以球O的表面积为
,所以球O的表面积为![]() ,所以该命题正确;
,所以该命题正确;
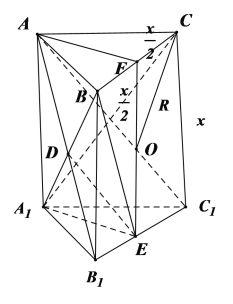
④,设![]() ,球的半径为
,球的半径为![]() ,设上底面和下底面的中心分别为
,设上底面和下底面的中心分别为![]() ,连接
,连接![]() ,则其中点为
,则其中点为![]() ,连接
,连接![]() .由题得
.由题得![]() 所以
所以![]() ,即
,即![]() ,又
,又![]() ,所以
,所以![]() ,所以
,所以![]() ,(当且仅当
,(当且仅当![]() 时取等),所以
时取等),所以![]() 最小值为2,所以球O体积的最小值为
最小值为2,所以球O体积的最小值为![]() ,所以该命题正确.
,所以该命题正确.
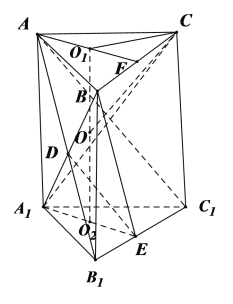
故选:D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目