题目内容
【题目】已知函数![]() ,在
,在![]() 上任取三个数
上任取三个数![]() ,均存在以
,均存在以![]() 为三边的三角形,则实数
为三边的三角形,则实数![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.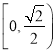
C.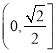 D.
D.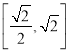
【答案】A
【解析】
试题分析:由题设可得对称轴方程![]() ,则
,则![]() ,则由题设三角形两边之和大于第三边可知最小值的两倍大于最大值,即
,则由题设三角形两边之和大于第三边可知最小值的两倍大于最大值,即![]() ,也即
,也即![]() ,解之得
,解之得![]() .故应选A.
.故应选A.
考点:二次函数的图象和性质及三角形的边角关系及运用.
【易错点晴】化归与转化的数学思想是高中数学中的重要数学思想方法之一,也是高考常考重要知识和考点之一.本题以函数![]() ,在
,在![]() 上任取三个数
上任取三个数![]() 为背景,考查的是函数值域的求法及等价转化的数学思想等有关知识和运算求解能力.解答时充分依据题设条件“存在以
为背景,考查的是函数值域的求法及等价转化的数学思想等有关知识和运算求解能力.解答时充分依据题设条件“存在以![]() 为三边的三角形”,然后将其等价转化为三角形两边之和大于第三边可知最小值的两倍大于最大值,建立不等式
为三边的三角形”,然后将其等价转化为三角形两边之和大于第三边可知最小值的两倍大于最大值,建立不等式![]() ,然后解不等式使得问题获解.
,然后解不等式使得问题获解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】一汽车![]() 店新进
店新进![]() 三类轿车,每类轿车的数量如下表:
三类轿车,每类轿车的数量如下表:
类别 |
|
|
|
数量 | 4 | 3 | 2 |
同一类轿车完全相同,现准备提取一部分车去参加车展.
(1)从店中一次随机提取2辆车,求提取的两辆车为同一类型车的概率;
(2)若一次性提取4辆车,其中![]() 三种型号的车辆数分别记为
三种型号的车辆数分别记为![]() ,记
,记![]() 为
为![]() 的最大值,求
的最大值,求![]() 的分布列和数学期望.
的分布列和数学期望.


