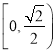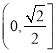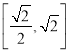题目内容
【题目】已知![]() (x≥0)成等差数列.又数列{an}(an>0)中,a1=3 ,此数列的前n项的和Sn(n∈N*)对所有大于1的正整数n都有Sn=f(Sn-1).
(x≥0)成等差数列.又数列{an}(an>0)中,a1=3 ,此数列的前n项的和Sn(n∈N*)对所有大于1的正整数n都有Sn=f(Sn-1).
(1)求数列{an}的第n+1项;
(2)若![]() 是
是![]() ,
,![]() 的等比中项,且Tn为{bn}的前n项和,求Tn.
的等比中项,且Tn为{bn}的前n项和,求Tn.
【答案】(1) an+1=6n+3(2) ![]()
【解析】
试题分析:(1)有![]() (x≥0)成等差数列,利用等差数列定义得到f(x)的函数解析式,再利用Sn=f(Sn-1)得到数列an的关于前n项和式子,在有前n项和求出数列的第n+1项;(2)由于
(x≥0)成等差数列,利用等差数列定义得到f(x)的函数解析式,再利用Sn=f(Sn-1)得到数列an的关于前n项和式子,在有前n项和求出数列的第n+1项;(2)由于![]() 是
是![]() ,
,![]() 的等比中项,所以可以利用等比中项的定义得到数列bn的通项公式,在利用裂项相消法可以求{bn}的前n项和Tn
的等比中项,所以可以利用等比中项的定义得到数列bn的通项公式,在利用裂项相消法可以求{bn}的前n项和Tn
试题解析:因为![]() ,
,![]() ,
,![]() (x≥0)成等差数列,所以
(x≥0)成等差数列,所以![]() ×2=
×2=![]() +
+![]() .
.
所以f(x)=(![]() +
+![]() )2.
)2.
因为Sn=f(Sn-1)(n≥2),
所以Sn=f(Sn-1)=(![]() +
+![]() )2.
)2.
所以![]() =
=![]() +
+![]() ,
,![]() -
-![]() =
=![]() .
.
所以{![]() }是以
}是以![]() 为公差的等差数列.
为公差的等差数列.
因为a1=3,所以S1=a1=3.
所以![]() =
=![]() +(n-1)
+(n-1) ![]() =
=![]() +
+![]() -
-![]() =
=![]() n.
n.
所以Sn=3n2(n∈N*).所以an+1=Sn+1-Sn=3(n+1)2-3n2=6n+3.
(2)因为数列![]() 是
是![]() ,
,![]() 的等比中项,
的等比中项,
所以(![]() )2=
)2=![]() ·
·![]() ,
,
所以bn=![]() =
=![]() =
=![]() .
.
所以Tn=b1+b2+…+bn=![]()

练习册系列答案
相关题目