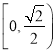题目内容
【题目】![]() 年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取
年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取![]() 名学生的数学成绩进行统计,将他们的成绩分成六段
名学生的数学成绩进行统计,将他们的成绩分成六段![]() 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.

(1)求这40名学生中数学成绩不低于120分的学生人数;
(2)若从数学成绩![]() 内的学生中任意抽取2人,求成绩在
内的学生中任意抽取2人,求成绩在![]() 中至少有一人的概率.
中至少有一人的概率.
【答案】(1)14;(2)![]() 。
。
【解析】
试题分析:(1)根据频率分布直方图可知,每个小长方形的面积等于该组相应的频率,所有小长方形面积和等于频率之和,等于1。成绩不低于120分的为最后两组,这两组的频率和为(0.025+0.010)×10=0.35,所以40名学生中,根据频率分布直方图估计,成绩不低于120分的人数为40×0.35=14人,本问考查频率分布直方图,属于对基础知识的考查。(2)根据频率分布直方图可知,成绩在[80,100)内的频率为(0.005+0.010)×10=0.15,人数为40×0.15=6人,期中成绩在[80,90)内的频率为0.010×10=0.1,人数为40×0.1=4人,设这四人编号为a,b,c,d,其余两人编号为e,f,从6人中任选2人,可以写出所有基本事件![]() ,
,![]() 共
共![]() 种.设成绩在
种.设成绩在![]() 的学生至少有一人为基本事件A,则事件A包含的基本事件如下:
的学生至少有一人为基本事件A,则事件A包含的基本事件如下:![]() 共9种,则根据古典概型概率公式,事件A的概率为
共9种,则根据古典概型概率公式,事件A的概率为![]() 。
。
试题解析:(1)(0.025+0.010)×10=0.35,人数为40×0.35=14人
(2)从图中知,成绩在![]() 的人数为
的人数为![]() (人), 成绩在
(人), 成绩在![]() 的人数为
的人数为![]() (人), 设成绩在
(人), 设成绩在![]() 的学生记为
的学生记为![]() ,成绩在
,成绩在![]() 的学生记为
的学生记为![]() .则从成绩在
.则从成绩在![]() 内的学生中任取
内的学生中任取![]() 人组成的基本事件有
人组成的基本事件有![]() ,
,![]() 共
共![]() 种.其中成绩在
种.其中成绩在![]() 的学生至少有一人的基本事件有
的学生至少有一人的基本事件有![]() 共9种.
共9种.
![]() 成绩在
成绩在![]() 的学生至少有一人的概率为
的学生至少有一人的概率为![]() .
.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目