题目内容
【题目】如图,四棱锥![]() ,底面
,底面![]() 是
是![]() 的菱形,侧面
的菱形,侧面![]() 是边长为
是边长为![]() 的正三角形,O是AD的中点,
的正三角形,O是AD的中点, ![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)若PO与底面ABCD垂直,求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(1)详见解析(2)![]()
【解析】
试题分析:(I)取AD中点 O,连接OP,OC,AC,证明OC⊥AD,OP⊥AD.推出AD⊥平面POC,即可在,PC⊥AD.(II)证明PO⊥平面ABCD.说明PO为三棱锥P-ACD的高.求出△PAC的面积,设点D到平面 PAC的距离为h,由VD-PAC=VP-ACD,求出点D到平面PAC的距离,然后求解直线DM与平面PAC所成的角的正弦值
试题解析:(1)连接![]() ,
,![]() ,
,
由题意可知![]() ,
,![]() 均为正三角形.
均为正三角形.
所以![]() ,
,![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
所以![]() .
.
(2)又![]() 平面
平面![]() .即
.即![]() 为三棱锥
为三棱锥![]() 的高.
的高.
在![]() 中,
中,![]() ,
,![]()
在![]() 中,
中,![]() ,
,![]() ,
,
边![]() 上的高
上的高![]() ,
,
所以![]() 的面积
的面积![]() .
.
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,由
,由![]() 得,
得,
![]() ,
,
又![]() ,
,
所以![]() ,解得
,解得![]() .
.
故点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
则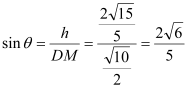 ,
,
所以直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目