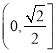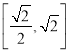Question

【题目】已知函数在区间[-1，4]上有最大值10和最小值1.设

（1）求的值;

（2）证明：函数在上是增函数.

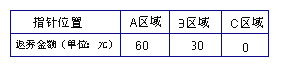
（3）若不等式在上有解,求实数的取值范围.

Answer 1

【答案】（1）（2）详见解析（3）

【解析】

试题分析：（1）根据函数的对称轴得到关于a的方程组，解出即可；（2）先求出g（x）的表达式，根据定义证明函数的单调性即可；（3）问题转化为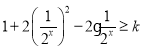，令，则k≤2t2-2t+1，构造新函数，结合函数的单调性从而求出k的范围即可

试题解析：（1）

因为a>0, 故,解得. ……………………4分

（2）由已知可得，设，

∵ …………………6分

∵，∴x1－x2＜0，2＜x1x2，即x1x2－2>0.

∴g（x1）－g（x2）<0，即g（x1）<g（x2）.

所以函数g（x）在上是增函数 ………………………………………8分

（3） 可化为,

化为令,则 ……………………10分

因,故

记因为,故，

所以k的取值范围是 ………………………………………………………12分