题目内容
设a1,a2, ,an为正整数,其中至少有五个不同值. 若对于任意的i,j(1≤i<j≤n),存在k,l(k≠l,且异于i与j)使得ai+aj=ak+al,则n的最小值是 .
13
试题分析:根据题意,设a1,a2, ,an为正整数,其中至少有五个不同值. 若对于任意的i,j(1≤i<j≤n),存在k,l(k≠l,且异于i与j)使得ai+aj=ak+al,那么对于n至少大于等于5,那么对于n从6开始,逐一的验证可知,那么最小的n为13.故答案为13.
点评:解决的关键是理解任意和存在的含义,并能对于n令值来分析推导得到结论,属于中档题。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
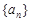 的通项公式
的通项公式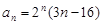 ,则数列
,则数列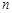 项和
项和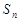 取得最小值时
取得最小值时



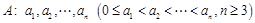 具有性质
具有性质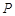 :
: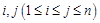 ,
,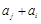 与
与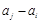 两数中至少有一个是该数列中的一项. 现给出以下四个命题:①数列
两数中至少有一个是该数列中的一项. 现给出以下四个命题:①数列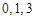 具有性质
具有性质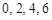 具有性质
具有性质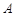 具有性质
具有性质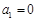 ;
; 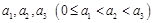 具有性质
具有性质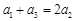 .
. 满足
满足 (
( )且
)且
 的值
的值 ,求
,求 的最小值及此时
的最小值及此时 的值
的值 ,则第2013个数是( )
,则第2013个数是( ) 满足
满足
 .定义:使乘积
.定义:使乘积 …
… 为正整数的
为正整数的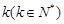 叫做“简易数”.则在
叫做“简易数”.则在 内所有“简易数”的和为 .
内所有“简易数”的和为 .  满足
满足 ,其中
,其中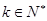 ,设
,设 ,则
,则 等于( ).
等于( ).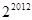
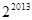


 是公差为
是公差为 的等差数列,且
的等差数列,且 成等比数列,则
成等比数列,则 项和
项和 为( )
为( )




 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )