题目内容
【题目】设实数![]() ,整数
,整数![]() ,
, ![]() .
.
(1)证明:当![]() 且
且![]() 时,
时, ![]() ;
;
(2)数列![]() 满足
满足![]() ,
, ![]() ,证明:
,证明: ![]() .
.
【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析.
【解析】试题分析; (1) 用数学归纳法证明即可;
(2) 先用数学归纳法证明![]() ,从
,从![]() 着手,由
着手,由![]() ,将求证式进行等价转化后即可解决,用相同的方式将
,将求证式进行等价转化后即可解决,用相同的方式将![]() 进行转换,设法利用已证结论证明.
进行转换,设法利用已证结论证明.
试题解析;
(Ⅰ) 证:用数学归纳法证明
(1)当![]() 时,
时, ![]() ,原不等式成立
,原不等式成立
(2)假设![]() 时,不等式
时,不等式![]() 成立
成立
当![]() 时,
时, ![]()
![]()
所以![]() 时,原不等式成立
时,原不等式成立
综合(1)(2),知当![]() 且
且![]() 时,对一切整数
时,对一切整数![]() ,不等式
,不等式![]() 均成立…
均成立…
(Ⅱ)先用数学归纳法证明![]() 。
。
(1)当![]() 时由假设
时由假设![]() 知
知![]() 成立。
成立。
(2)假设![]() 时,不等式
时,不等式![]() 成立
成立
由![]() 易知
易知![]()
当![]() 时
时
由![]() 得
得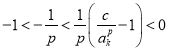
由(Ⅰ)中的结论得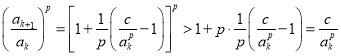
因此![]() ,即
,即![]() ,所以当
,所以当![]() 时,不等式
时,不等式![]() 也成立
也成立
综合(1)(2)可得,对一切正整数![]() ,不等式
,不等式![]() 均成立
均成立
再由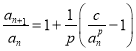 得
得![]() ,即
,即![]()
综上所述, ![]()

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
【题目】调查在![]() 级风的海上航行中71名乘客的晕船情况,在男人中有12人晕船,25人不晕船,在女人中有10人晕船,24人不晕船
级风的海上航行中71名乘客的晕船情况,在男人中有12人晕船,25人不晕船,在女人中有10人晕船,24人不晕船
(1)作出性别与晕船关系的列联表;
(2)根据此资料,能否在犯错误的概率不超过0.1的前提下认为![]() 级风的海上航行中晕船与性别有关?
级风的海上航行中晕船与性别有关?
晕船 | 不晕船 | 总计 | |
男人 | |||
女人 | |||
总计 |
附:.![]()
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |