题目内容
【题目】已知椭圆C: ![]() (a>b>0)的焦距为
(a>b>0)的焦距为![]() ,且椭圆C过点A(1,
,且椭圆C过点A(1, ![]() ),
),
(Ⅰ)求椭圆C的方程;
(Ⅱ)若O是坐标原点,不经过原点的直线L:y=kx+m与椭圆交于两不同点P(x1,y1),Q(x2,y2),且y1y2=k2x1x2,求直线L的斜率k;
(Ⅲ)在(Ⅱ)的条件下,求△OPQ面积的最大值.
【答案】(I)![]() ;(Ⅱ)斜率为
;(Ⅱ)斜率为![]() 或﹣
或﹣![]() ;(Ⅲ)1.
;(Ⅲ)1.
【解析】试题分析:(1)由椭圆的焦距为![]() ,且椭圆C过点A(1,
,且椭圆C过点A(1, ![]() ),列出方程求出a,b,由此能求出椭圆C的方程.
),列出方程求出a,b,由此能求出椭圆C的方程.
(2)由![]() ,得: (1+4k2)x2+8kmx+4(m2﹣1)=0,由此利用根的判别式、韦达定理,结合已知条件能求出直线l的斜率.
,得: (1+4k2)x2+8kmx+4(m2﹣1)=0,由此利用根的判别式、韦达定理,结合已知条件能求出直线l的斜率.
(3)把直线方程![]() 与椭圆方程
与椭圆方程![]() 联立,得: x2+2mx+2m2﹣2=0,,由此利用根的判别式、韦达定理、点到直线距离公式、弦长公式能求出△OPQ 面积的最大值.
联立,得: x2+2mx+2m2﹣2=0,,由此利用根的判别式、韦达定理、点到直线距离公式、弦长公式能求出△OPQ 面积的最大值.
试题解析:
(Ⅰ)∵椭圆C: ![]() 的焦距为
的焦距为![]() ,且椭圆C过点
,且椭圆C过点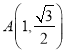 ,
,
∴由题意得![]() ,可设椭圆方程为
,可设椭圆方程为![]() ,
,
则![]() ,得
,得![]() ,
,
所以椭圆C的方程为![]() .
.
(Ⅱ)由![]() 消去y得:(1+4k2)x2+8kmx+4(m2﹣1)=0,
消去y得:(1+4k2)x2+8kmx+4(m2﹣1)=0,
△=64k2m2﹣16(1+4k2)(m2﹣1)=16(4k2﹣m2+1)>0,
![]() ,
,
故![]() .
.
又∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵m≠0,∴![]() ,解得
,解得![]() ,
,
∴直线L的斜率为![]() 或﹣
或﹣![]() .
.
(Ⅲ)由(Ⅱ)可知直线L的方程为![]()
由对称性,不妨把直线方程![]() 与椭圆方程
与椭圆方程![]() 联立,消去y得:2x2+4mx+4m2﹣4=0,△=64m2﹣4(4m2﹣4)>0,∵P(x1,y1),Q(x2,y2),∴x1+x2=﹣2m,
联立,消去y得:2x2+4mx+4m2﹣4=0,△=64m2﹣4(4m2﹣4)>0,∵P(x1,y1),Q(x2,y2),∴x1+x2=﹣2m, ![]() ,
,
设d为点O到直线l的距离,则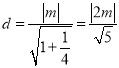 ,
,
![]()
当且仅当m2=1时,等号成立.∴△OPQ面积的最大值为1.

【题目】某地区2010年至2016年农村居民家庭纯收入![]() (单位:千元)的数据如下表
(单位:千元)的数据如下表
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求![]() 关于
关于![]() 的线性回归方程。
的线性回归方程。
(2)判断![]() 与
与![]() 之间是正相关还是负相关?
之间是正相关还是负相关?
(3)预测该地区2018年农村居民家庭人均纯收入。
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
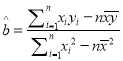 ,
, ![]()