题目内容
【题目】已知直线![]() ,若存在实数
,若存在实数![]() 使得一条曲线与直线
使得一条曲线与直线![]() 由两个不同的交点,且以这两个交点为端点的线段长度恰好等于
由两个不同的交点,且以这两个交点为端点的线段长度恰好等于![]() ,则称此曲线为直线
,则称此曲线为直线![]() 的“绝对曲线”.下面给出的四条曲线方程:
的“绝对曲线”.下面给出的四条曲线方程:
①![]() ;②
;② ![]() ;③
;③![]() ;④
;④![]() .
.
其中直线![]() 的“绝对曲线”的条数为( )
的“绝对曲线”的条数为( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】依题意可知,直线![]() 恒过定点
恒过定点![]() .对于①,函数
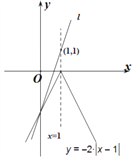
.对于①,函数![]() 的图象关于直线
的图象关于直线![]() 对称,如图所示,所以直线
对称,如图所示,所以直线![]() 与其只能有一个交点,故满足题意的
与其只能有一个交点,故满足题意的![]() 不存在,故① 不符合题意;
不存在,故① 不符合题意;
对于② ,方程![]() 的图象为以点
的图象为以点![]() 为圆心的圆,因此直线
为圆心的圆,因此直线![]() 过圆心,直线与圆两个交点所组成的线段长为
过圆心,直线与圆两个交点所组成的线段长为![]() ,故当
,故当![]() ,直线
,直线![]() 或
或![]() ,直线斜率的绝对值等于截线段长度,即
,直线斜率的绝对值等于截线段长度,即![]() 存在,故② 符合题意;对于③ ,此曲线为一个椭圆,定点
存在,故② 符合题意;对于③ ,此曲线为一个椭圆,定点![]() 在椭圆上,将直线方程代入可得
在椭圆上,将直线方程代入可得![]() ,所以
,所以![]() ,若曲线是直线的“绝对曲线”,则
,若曲线是直线的“绝对曲线”,则![]() ,即
,即![]() ,化简得
,化简得![]() ,令
,令![]() ,则问题转化为存在
,则问题转化为存在![]() ,使得
,使得![]() 成立,因为
成立,因为![]() ,且
,且![]() 为连续函数,所以在区间
为连续函数,所以在区间![]() 存在零点,即
存在零点,即![]() 存在实根,故③符合题意;对于④,首先明确两个极限情况:
存在实根,故③符合题意;对于④,首先明确两个极限情况: ![]() ,此时斜率绝对值无穷大,截线段长度为有限值;
,此时斜率绝对值无穷大,截线段长度为有限值; ![]() ,此时斜率绝对值为零,且当斜率绝对值趋于零时,截线段长度趋于无穷大;若将直线
,此时斜率绝对值为零,且当斜率绝对值趋于零时,截线段长度趋于无穷大;若将直线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,可见斜率绝对值变化趋势为由正无穷单调递减至零,截线段长度变化趋势为从一有限值趋于正无穷(变化过程不一定单调),设
,可见斜率绝对值变化趋势为由正无穷单调递减至零,截线段长度变化趋势为从一有限值趋于正无穷(变化过程不一定单调),设![]() 为斜率绝对值变化情况,
为斜率绝对值变化情况, ![]() 为线段长度变化情况,
为线段长度变化情况, ![]() 为转动角度,做出示意图如下:
为转动角度,做出示意图如下:

必存在某一转动角度![]() 使得
使得![]() 与图象
与图象![]() 相交,即存在
相交,即存在![]() 使得直线斜率的绝对值等于截线段长度,故④符合题意,直线
使得直线斜率的绝对值等于截线段长度,故④符合题意,直线![]() 的“绝对曲线”的条数为4,故选C.
的“绝对曲线”的条数为4,故选C.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目