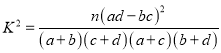题目内容

【题目】已知抛物线的焦点为，准线为，抛物线上一点的横坐标为1，且到焦点的距离为2.

（1）求抛物线的方程；

（2）设是抛物线上异于原点的两个不同点，直线和的倾斜角分别为和，当变化且为定值时，证明直线恒过定点，并求出该定点的坐标.

【答案】（1）；（2）.

【解析】试题分析：（1）由抛物线的定义求解即可；

（2）设点，设直线的方程分别为与抛物线联立求交点，用坐标表示斜率，斜率表示正切研究即可.

试题解析：

（1）由抛物线的定义知，点到焦点的距离等于到准线的距离，所以.故抛物线的标准方程为.

（2）设点，由题意得 (否则,不满足)，且，

设直线的方程分别为，

联立解得；联立，解得.

则由两点式得直线的方程为.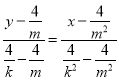

化简得.①

因为，且得,

可得.②

将②代人①，化简得 ，

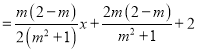即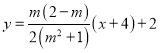,令,得.

所以直线恒过定点.

练习册系列答案
相关题目

【题目】在一次抽样调查中测得样本的6组数据，得到一个变量关于的回归方程模型，其对应的数值如下表：

2

3

4

5

6

7

(1)请用相关系数加以说明与之间存在线性相关关系(当时，说明与之间具有线性相关关系)；

(2)根据(1)的判断结果，建立关于的回归方程并预测当时，对应的值为多少(精确到).

附参考公式：回归方程中斜率和截距的最小二乘法估计公式分别为：

，，相关系数公式为：.

参考数据：

，，，.

【题目】已知函数为实数)的图像在点处的切线方程为.

（1）求实数的值及函数的单调区间；

（2）设函数，证明时， .

【题目】传承传统文化再掀热潮，央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏。将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级，随即从中抽取了100名选手进行调查，下面是根据调查结果绘制的选手等级人数的条形图.

（Ⅰ）若将一般等级和良好等级合称为合格等级，根据已知条件完成下面的列联表，并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关？

注：其中.

（Ⅱ）在优秀等级的选手中取6名，依次编号为1,2,3,4,5,6，在良好等级的选手中取6名，依次编号为1,2,3,4,5,6，在选出的6名优秀等级的选手中任取一名，记其编号为，在选出的6名良好等级的选手中任取一名，记其编号为，求使得方程组有唯一一组实数解的概率.

【题目】已知函数且.

（1）当时，求函数的单调区间与极值；

（2）当时， 恒成立，求的取值范围.

【题目】已知椭圆C： （a＞b＞0）的焦距为，且椭圆C过点A（1， ），

（Ⅰ）求椭圆C的方程；

（Ⅱ）若O是坐标原点，不经过原点的直线L：y=kx+m与椭圆交于两不同点P（x1，y1），Q（x2，y2），且y1y2=k2x1x2，求直线L的斜率k；

（Ⅲ）在（Ⅱ）的条件下，求△OPQ面积的最大值．

【题目】如图：区域A是正方形OABC（含边界），区域B是三角形ABC（含边界）。

（Ⅰ）向区域A随机抛掷一粒黄豆，求黄豆落在区域B的概率；

（Ⅱ）若x,y分别表示甲、乙两人各掷一次骰子所得的点数，求点（x，y）落在区域B的概率；

【题目】已知数列{an}满足an+1= an+t，a1= （t为常数，且t≠ ）．
（1）证明：{an﹣2t}为等比数列；
（2）当t=﹣ 时，求数列{an}的前几项和最大？
（3）当t=0时，设cn=4an+1，数列{cn}的前n项和为Tn ， 若不等式 ≥2n﹣7对任意的n∈N*恒成立，求实数k的取值范围．

【题目】设是等差数列，是等比数列，且，则下列结论正确的是（ ）

A. B.

C. D. ，使得

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网