题目内容
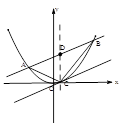
如图,抛物线关于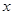 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点 、
、 、
、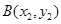 均在抛物线上.
均在抛物线上.
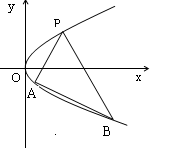
(1)写出该抛物线的方程及其准线方程;
(2)当 与
与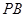 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求 的值及直线
的值及直线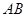 的斜率.
的斜率.
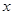 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点 、
、 、
、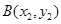 均在抛物线上.
均在抛物线上.
(1)写出该抛物线的方程及其准线方程;
(2)当
 与
与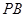 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求 的值及直线
的值及直线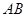 的斜率.
的斜率.(1)故所求抛物线的方程是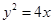 ,准线方程是
,准线方程是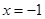 ;(2)
;(2)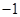 .
.
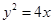 ,准线方程是
,准线方程是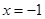 ;(2)
;(2)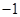 .
.试题分析:(I)设出抛物线的方程,把点P代入抛物线求得p则抛物线的方程可得,进而求得抛物线的准线方程.
(2)设直线PA的斜率为
 ,直线PB的斜率为
,直线PB的斜率为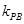 ,则可分别表示
,则可分别表示 和
和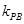 ,根据倾斜角互补可知
,根据倾斜角互补可知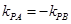 ,进而求得
,进而求得 的值,把A,B代入抛物线方程两式相减后即可求得直线AB的斜率.
的值,把A,B代入抛物线方程两式相减后即可求得直线AB的斜率. 试题解析:(I)由已知条件,可设抛物线的方程为
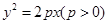
因为点
 在抛物线上,所以
在抛物线上,所以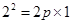 ,得
,得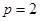 . 2分
. 2分故所求抛物线的方程是
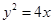 , 准线方程是
, 准线方程是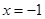 . 4分
. 4分(2)设直线
 的方程为
的方程为 ,
,即:
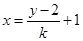 ,代入
,代入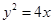 ,消去
,消去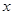 得:
得: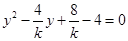 . 5分
. 5分设
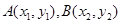 ,由韦达定理得:
,由韦达定理得: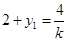 ,即:
,即: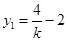 . 7分
. 7分将
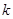 换成
换成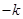 ,得
,得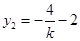 ,从而得:
,从而得: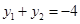 , 9分
, 9分直线
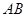 的斜率
的斜率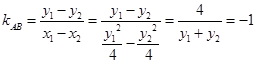 . 12分.
. 12分.
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
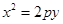
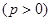 上的点
上的点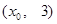 到焦点的距离等于4,直线
到焦点的距离等于4,直线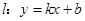 与抛物线相交于不同的两点
与抛物线相交于不同的两点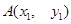 、
、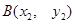 ,且
,且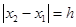 (
(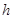 为定值).设线段
为定值).设线段 的中点为
的中点为 ,与直线
,与直线 ..
..
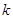 、
、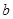 表示出
表示出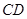 垂直于
垂直于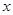 轴;
轴;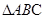 的面积,证明
的面积,证明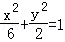 的右焦点重合,则p的值为( )
的右焦点重合,则p的值为( )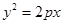 (
(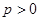 )的焦点为
)的焦点为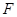 ,准线为
,准线为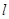 ,
,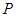 为抛物线上一点,
为抛物线上一点,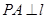 ,垂足为
,垂足为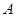 .如果
.如果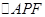 是边长为
是边长为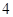 的正三角形,则此抛物线的焦点坐标为__________,点
的正三角形,则此抛物线的焦点坐标为__________,点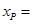 ______.
______.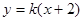 (k>0)与抛物线
(k>0)与抛物线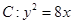 相交于
相交于 、
、 两点,
两点,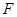 为
为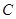 的焦点,若
的焦点,若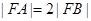 ,则k的值为
,则k的值为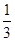
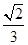
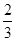
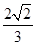
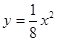 的焦点坐标为( )
的焦点坐标为( )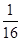 )
)
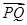 =λ
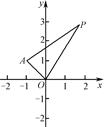
=λ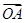 ,直线OP与QA交于点M,问:是否存在点P,使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由.
,直线OP与QA交于点M,问:是否存在点P,使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由.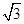 x,△AOB的面积为6
x,△AOB的面积为6