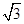题目内容
在平面直角坐标系xOy中,已知点A(-1,1),P是动点,且△POA的三边所在直线的斜率满足kOP+kOA=kPA.
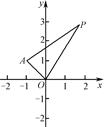
(1)求点P的轨迹C的方程;
(2)若Q是轨迹C上异于点P的一个点,且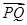 =λ
=λ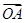 ,直线OP与QA交于点M,问:是否存在点P,使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由.
,直线OP与QA交于点M,问:是否存在点P,使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由.

(1)求点P的轨迹C的方程;
(2)若Q是轨迹C上异于点P的一个点,且
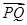 =λ
=λ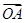 ,直线OP与QA交于点M,问:是否存在点P,使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由.
,直线OP与QA交于点M,问:是否存在点P,使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由.(1)y=x2(x≠0且x≠-1)(2)(1,1)
(1)设点P(x,y)为所求轨迹上的任意一点,则由kOP+kOA=kPA得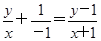 ,
,
整理得轨迹C的方程为y=x2(x≠0且x≠-1).
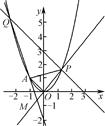
(2)设P(x1,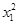 ),Q(x2,
),Q(x2,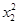 ,M(x0,y0),
,M(x0,y0),
由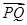 =λ
=λ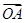 可知直线PQ∥OA,则kPQ=kOA,故
可知直线PQ∥OA,则kPQ=kOA,故 ,即x2+x1=-1,
,即x2+x1=-1,
由O、M、P三点共线可知, =(x0,y0)与
=(x0,y0)与 =(x1,
=(x1,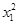 )共线,
)共线,
∴x0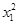 -x1y0=0,由(1)知x1≠0,故y0=x0x1,
-x1y0=0,由(1)知x1≠0,故y0=x0x1,
同理,由 =(x0+1,y0-1)与
=(x0+1,y0-1)与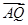 =(x2+1,
=(x2+1,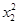 -1)共线可知(x0+1)(
-1)共线可知(x0+1)(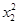 -1)-(x2+1)(y0-1)=0,即(x2+1)[(x0+1)·(x2-1)-(y0-1)]=0,
-1)-(x2+1)(y0-1)=0,即(x2+1)[(x0+1)·(x2-1)-(y0-1)]=0,
由(1)知x2≠-1,故(x0+1)(x2-1)-(y0-1)=0,
将y0=x0x1,x2=-1-x1代入上式得(x0+1)(-2-x1)-(x0x1-1)=0,
整理得-2x0(x1+1)=x1+1,由x1≠-1得x0=-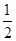 ,由S△PQA=2S△PAM,得到QA=2AM,
,由S△PQA=2S△PAM,得到QA=2AM,
∵PQ∥OA,∴OP=2OM,∴ =2
=2 ,∴x1=1,∴P的坐标为(1,1)
,∴x1=1,∴P的坐标为(1,1)
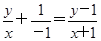 ,
,整理得轨迹C的方程为y=x2(x≠0且x≠-1).

(2)设P(x1,
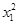 ),Q(x2,
),Q(x2,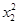 ,M(x0,y0),
,M(x0,y0),由
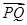 =λ
=λ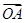 可知直线PQ∥OA,则kPQ=kOA,故
可知直线PQ∥OA,则kPQ=kOA,故 ,即x2+x1=-1,
,即x2+x1=-1,由O、M、P三点共线可知,
 =(x0,y0)与
=(x0,y0)与 =(x1,
=(x1,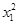 )共线,
)共线,∴x0
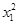 -x1y0=0,由(1)知x1≠0,故y0=x0x1,
-x1y0=0,由(1)知x1≠0,故y0=x0x1,同理,由
 =(x0+1,y0-1)与
=(x0+1,y0-1)与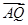 =(x2+1,
=(x2+1,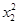 -1)共线可知(x0+1)(
-1)共线可知(x0+1)(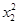 -1)-(x2+1)(y0-1)=0,即(x2+1)[(x0+1)·(x2-1)-(y0-1)]=0,
-1)-(x2+1)(y0-1)=0,即(x2+1)[(x0+1)·(x2-1)-(y0-1)]=0,由(1)知x2≠-1,故(x0+1)(x2-1)-(y0-1)=0,
将y0=x0x1,x2=-1-x1代入上式得(x0+1)(-2-x1)-(x0x1-1)=0,
整理得-2x0(x1+1)=x1+1,由x1≠-1得x0=-
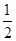 ,由S△PQA=2S△PAM,得到QA=2AM,
,由S△PQA=2S△PAM,得到QA=2AM,∵PQ∥OA,∴OP=2OM,∴
 =2
=2 ,∴x1=1,∴P的坐标为(1,1)
,∴x1=1,∴P的坐标为(1,1)
练习册系列答案
相关题目
 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点 、
、 、
、 均在抛物线上.
均在抛物线上.
 与
与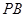 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求 的值及直线
的值及直线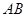 的斜率.
的斜率.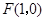 ,直线
,直线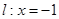 ,
,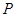 为平面上的动点,过点
为平面上的动点,过点 的垂线,垂足为点
的垂线,垂足为点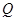 ,且
,且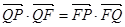 .
. 的方程;
的方程;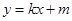 与曲线
与曲线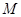 ,且与直线
,且与直线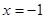 相交于点
相交于点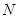 ,试探究:在坐标平面内是否存在一个定点
,试探究:在坐标平面内是否存在一个定点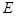 ,使得以
,使得以 为直径的圆恒过此定点
为直径的圆恒过此定点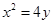 的焦点作直线l交抛物线于A,B两点,分别过A,B作抛物线的切线
的焦点作直线l交抛物线于A,B两点,分别过A,B作抛物线的切线 ,则
,则 与
与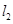 的交点P的轨迹方程是( )
的交点P的轨迹方程是( )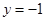
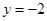

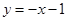
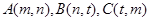 ,直线AC的斜率与倾斜角为钝角的直线AB的斜率之和为
,直线AC的斜率与倾斜角为钝角的直线AB的斜率之和为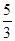 ,而直线AB恰好经过抛物线
,而直线AB恰好经过抛物线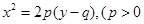 )的焦点F并且与抛物线交于P、Q两点(P在Y轴左侧).则
)的焦点F并且与抛物线交于P、Q两点(P在Y轴左侧).则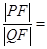 ( )
( )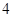
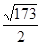

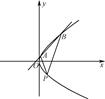
 x的焦点,P为C上一点,若|PF|=4
x的焦点,P为C上一点,若|PF|=4