题目内容
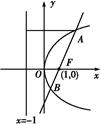
过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点.若|AF|=3,则|BF|= .
由题意知,抛物线的焦点F的坐标为(1,0),又|AF|=3,由抛物线定义知,点A到准线x=-1的距离为3
∴点A的横坐标为2.
将x=2代入y2=4x得y2=8,
由图知点A的纵坐标y=2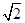 ,
,
∴A(2,2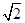 ),
),
∴直线AF的方程为y=2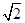 (x-1).
(x-1).
由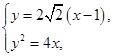 解得
解得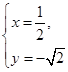 或
或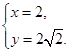
由图知,点B的坐标为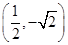 ,
,
∴|BF|=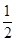 -(-1)=
-(-1)=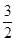 .
.

∴点A的横坐标为2.
将x=2代入y2=4x得y2=8,
由图知点A的纵坐标y=2
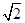 ,
,∴A(2,2
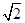 ),
),∴直线AF的方程为y=2
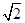 (x-1).
(x-1).由
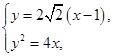 解得
解得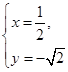 或
或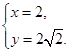
由图知,点B的坐标为
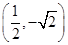 ,
,∴|BF|=
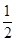 -(-1)=
-(-1)=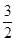 .
.
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
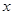 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点 、
、 、
、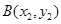 均在抛物线上.
均在抛物线上.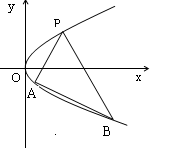
 与
与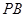 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求 的值及直线
的值及直线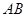 的斜率.
的斜率.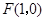 ,直线
,直线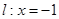 ,
,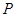 为平面上的动点,过点
为平面上的动点,过点 的垂线,垂足为点
的垂线,垂足为点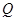 ,且
,且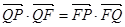 .
. 的方程;
的方程;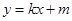 与曲线
与曲线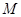 ,且与直线
,且与直线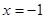 相交于点
相交于点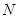 ,试探究:在坐标平面内是否存在一个定点
,试探究:在坐标平面内是否存在一个定点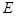 ,使得以
,使得以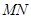 为直径的圆恒过此定点
为直径的圆恒过此定点 与
与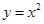 交于
交于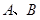 两点,若使得以
两点,若使得以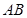 为直径的圆过原点,则直线
为直径的圆过原点,则直线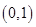
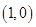
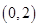

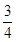

 x的焦点,P为C上一点,若|PF|=4
x的焦点,P为C上一点,若|PF|=4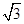
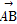 ·
·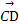 的值是 .
的值是 .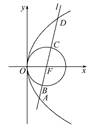
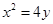 ,下列描述正确的是
,下列描述正确的是