题目内容
13．求下列椭圆的焦点坐标：（1）$\frac{{x}^{2}}{100}+\frac{{y}^{2}}{36}=1$；
（2）2x2+y2=8．
分析 （1）求得椭圆的a，b，c，由焦点在x轴上，即可得到焦点坐标；
（2）先化为椭圆的标准方程，再求出a，b，c，确定焦点在y轴上，即可得到焦点坐标．
解答 解：（1）$\frac{{x}^{2}}{100}+\frac{{y}^{2}}{36}=1$的a=10，b=6，
焦点在x轴上，
c=$\sqrt{100-36}$=8，
则焦点坐标为（-8，0），（8，0）；
（2）2x2+y2=8，即为
$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{8}$=1，
由a2=8，b2=4，可得焦点在y轴上，
c=$\sqrt{8-4}$=2，
即有焦点的坐标为（0，2），（0，-2）．
点评 本题考查椭圆的焦点坐标，注意化为椭圆的标准方程，考查运算能力，属于基础题．
练习册系列答案
相关题目
4．
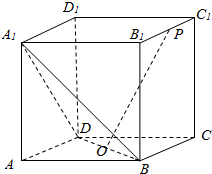如图，在正方体ABCD-A1B1C1D1中，点O为线段BD的中点．设点P在线段B1C1上，直线OP与平面A1BD所成的角为α，则sinα的取值范围是（ ）
如图，在正方体ABCD-A1B1C1D1中，点O为线段BD的中点．设点P在线段B1C1上，直线OP与平面A1BD所成的角为α，则sinα的取值范围是（ ）| A． | $[\frac{{\sqrt{6}}}{3}，1]$ | B． | $[\frac{{\sqrt{2}}}{3}，1]$ | C． | $[\frac{{\sqrt{2}}}{3}，\frac{{2\sqrt{2}}}{3}]$ | D． | $[\frac{{\sqrt{6}}}{3}，\frac{{2\sqrt{2}}}{3}]$ |
8．已知等差数列{an}为递增数列且满足a1+a10=10，则a5的取值范围是（ ）
| A． | （5，10） | B． | （5，+∞） | C． | （-∞，5） | D． | （10，+∞） |