题目内容
【题目】设双曲线C的焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,其一个顶点的坐标是(0,1).
,其一个顶点的坐标是(0,1).
(Ⅰ)求双曲线C的标准方程;
(Ⅱ)若直线![]() 与该双曲线交于A、B两点,且A、B的中点为(2,3),求直线
与该双曲线交于A、B两点,且A、B的中点为(2,3),求直线![]() 的方程
的方程
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(Ⅰ)由顶点坐标是(0,3),求得a,由已知条件双曲线的离心率为![]() ,列出方程求出c,利用双曲线的三参数的关系,求出b,据双曲线焦点的位置写出双曲线的方程.
,列出方程求出c,利用双曲线的三参数的关系,求出b,据双曲线焦点的位置写出双曲线的方程.
(Ⅱ)设出A,B的坐标,代入双曲线方程,两式相减,根据中点的坐标可知x1+x2和y1+y2的值,进而求得直线AB的斜率,根据点斜式求得直线的方程.
试题解析:
(1)由已知得 ![]()
又![]() ∴
∴![]()
∴ 双曲线C的标准方程为![]()
(2) 设A、B两点的坐标分别为![]() 、
、![]() ,
,
则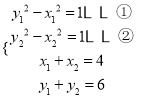 由①-②得:
由①-②得: ![]()
∴![]() .
.
∴直线![]() 的方程为
的方程为![]() 经检验满足。
经检验满足。

 阅读快车系列答案
阅读快车系列答案【题目】网购已经成为一种时尚,商家为了鼓励消费,购买时在店铺领取优惠券,买后给予好评返还现金等促销手段.经统计,近五年某店铺用于促销的费用![]() (万元)与当年度该店铺的销售收人
(万元)与当年度该店铺的销售收人![]() (万元)的数据如下表:
(万元)的数据如下表:
年份 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 |
促销费用 |
|
|
|
|
|
销售收入 |
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出/span>![]() 关于
关于![]() 的线性回归方
的线性回归方![]() ;
;
(2)2018年度该店铺预测销售收人至少达到![]() 万元,则该店铺至少准备投入多少万元的促销费?
万元,则该店铺至少准备投入多少万元的促销费?
参考公式: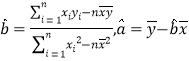
参考数据: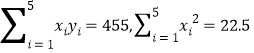
【题目】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表。
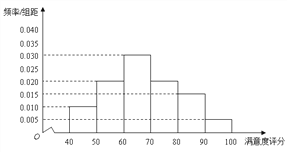
A地区用户满意度评分的频率分布直方图

B地区用户满意度评分的频数分布表
(Ⅰ)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
估计哪个地区的满意度等级为不满意的概率大?说明理由


