题目内容
【题目】已知![]() 的图像可由
的图像可由![]() 的图像平移得到,对于任意的实数
的图像平移得到,对于任意的实数![]() ,均有
,均有![]() 成立,且存在实数
成立,且存在实数![]() ,使得
,使得![]() 为奇函数.
为奇函数.
(Ⅰ)求函数![]() 的解析式.
的解析式.
(Ⅱ)函数![]() 的图像与直线
的图像与直线![]() 有两个不同的交点
有两个不同的交点![]() ,
, ![]() ,若
,若![]() ,
,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2) 实数
;(2) 实数![]() 的取值范围是
的取值范围是![]() .
.
【解析】
分析:(Ⅰ)根据题意![]() 的图像关系
的图像关系![]() 对称,
对称,![]() 关于
关于![]() 对称,
对称,
可设![]() ,
,
又根据存在实数![]() ,使得
,使得![]() 为奇函数,可求函数
为奇函数,可求函数![]() 的解析式.
的解析式.
(Ⅱ)根据题意![]() 的图像与
的图像与![]() 有两个不同交点,
有两个不同交点,
则![]() 有两个解,由
有两个解,由![]() ,解得:
,解得:![]() 或
或![]() ,
,
∵![]() ,
,![]() ,
,![]() ,直线
,直线![]() 恒过定点
恒过定点![]() 和
和![]() 连线的斜率为
连线的斜率为![]() ,∴
,∴![]() .符合
.符合![]()
详解:
(Ⅰ)![]() 的图像关系
的图像关系![]() 对称,
对称,![]() 关于
关于![]() 对称,
对称,
∴可设![]()
![]()
![]() ,
,
又存在实数![]() ,使得
,使得![]() 为奇函数,
为奇函数,
∴![]() 不含常数项.
不含常数项.
故![]() .
.
(Ⅱ)∵![]() 的图像与
的图像与![]() 有两个不同交点,
有两个不同交点,
∴![]() 有两个解,
有两个解,
∴![]() ,
,
解得:![]() 或
或![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() 连线的斜率为
连线的斜率为![]() ,
,
∴![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
【题目】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表。
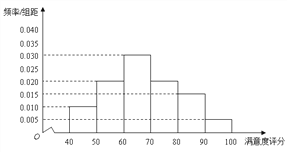
A地区用户满意度评分的频率分布直方图

B地区用户满意度评分的频数分布表
(Ⅰ)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
估计哪个地区的满意度等级为不满意的概率大?说明理由


