题目内容
3.b,c表示两条不重合的直线,α,β表示两个不重合的平面,下列命题中正确的是( )| A. | $\left.\begin{array}{l}{c∥α}\\{b?α}\end{array}\right\}$⇒c∥b | B. | $\left.\begin{array}{l}{c∥α}\\{α⊥β}\end{array}\right\}$⇒c⊥β | C. | $\left.\begin{array}{l}{c⊥α}\\{c⊥β}\end{array}\right\}$⇒α∥β | D. | $\left.\begin{array}{l}{b∥c}\\{c?α}\end{array}\right\}$⇒b∥α |
分析 利用线面平行、线面垂直的性质定理和判定定理对选项分别分析选择.
解答 解:选项A,由已知条件可得直线c,b平行或者异面;故A错误;
选项B,由已知可得直线c可能与平面β平行;故B 错误;
选项C,由已知,根据线面垂直的性质定理可以判断平面α与β平行;故C 正确;
选项D,由已知条件还可以得到直线B在平面α内;故D错误;
故选C.
点评 本题考查了线面平行、线面垂直的性质定理和判定定理的运用,熟练掌握定理的条件,正确运用是关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
14.某几何体的三视图如图所示,则该几何体的外接球的体积为( )
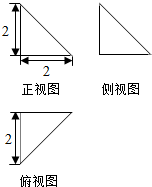

| A. | 4$\sqrt{3}$π | B. | $\frac{4\sqrt{3}π}{3}$ | C. | 4$\sqrt{2}$π | D. | $\frac{4\sqrt{2}π}{3}$ |
18.要得到函数y=tan(3x+$\frac{π}{3}$)的图象,只须将x=tan3x的图象上的所有的点( )
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{9}$个单位长度 | D. | 向右平移$\frac{π}{9}$个单位长度 |
15.设点P是Z轴上一点,且点P到M(1,0,2)与点N(1,-3,1)的距离相等,则点P的坐标是( )
| A. | (-3,-3,0) | B. | (0,0,3) | C. | (0,-3,-3) | D. | (0,0,-3) |