题目内容
已知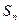 为数列
为数列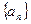 的前
的前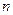 项和,
项和,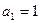 ,
,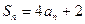 .
.
⑴设数列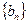 中,
中,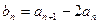 ,求证:
,求证: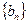 是等比数列;
是等比数列;
⑵设数列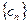 中,
中,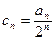 ,求证:
,求证: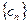 是等差数列;
是等差数列;
⑶求数列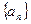 的通项公式及前
的通项公式及前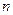 项和.
项和.
【解题思路】由于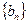 和
和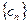 中的项与
中的项与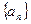 中的项有关,且
中的项有关,且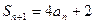 ,可利用
,可利用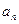 、
、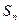 的关系作为切入点.
的关系作为切入点.
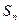 为数列
为数列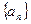 的前
的前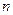 项和,
项和,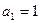 ,
,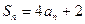 .
.⑴设数列
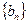 中,
中,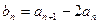 ,求证:
,求证: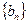 是等比数列;
是等比数列;⑵设数列
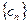 中,
中,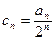 ,求证:
,求证: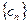 是等差数列;
是等差数列;⑶求数列
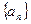 的通项公式及前
的通项公式及前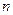 项和.
项和.【解题思路】由于
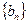 和
和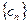 中的项与
中的项与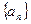 中的项有关,且
中的项有关,且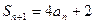 ,可利用
,可利用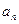 、
、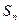 的关系作为切入点.
的关系作为切入点.⑴证明略⑵证明略⑶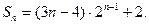
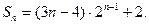
⑴
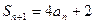 ,
,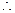
 ,两式相减,得
,两式相减,得
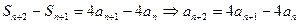 ,
,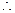
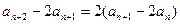
又
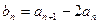 ,
,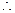
 ,由
,由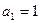 ,
,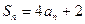 ,得
,得 
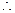
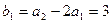 ,
,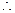
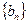 是等比数列,
是等比数列,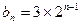 .
.
⑵由⑴知, ,且
,且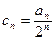
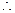
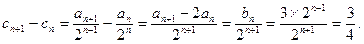
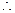
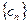 是等差数列,
是等差数列,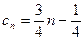 .
.
⑶
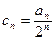 ,且
,且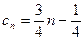 ,
,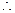
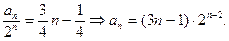
当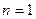 时,
时, ,
,
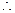
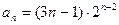 ,
,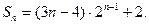
【名师指引】⑴等差、等比数列的证明方法主要有定义法、中项法;⑵将“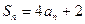 ”化归为
”化归为
 是解题的关键.
是解题的关键.

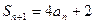 ,
,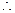
 ,两式相减,得
,两式相减,得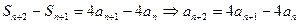 ,
,
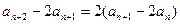
又

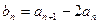 ,
,
 ,由
,由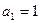 ,
,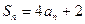 ,得
,得 
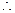
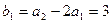 ,
,
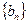 是等比数列,
是等比数列,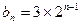 .
.⑵由⑴知,
 ,且
,且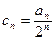
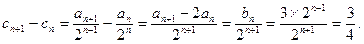
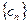 是等差数列,
是等差数列,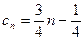 .
.⑶

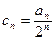 ,且
,且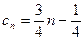 ,
,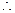
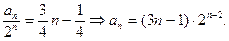
当
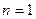 时,
时, ,
,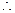
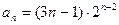 ,
,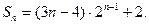
【名师指引】⑴等差、等比数列的证明方法主要有定义法、中项法;⑵将“
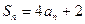 ”化归为
”化归为 是解题的关键.
是解题的关键.
练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
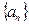 满足
满足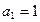 ,
,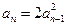 (n≥2).求数列
(n≥2).求数列 “2001年国内生产总值达到95933亿元,比上年增长7
“2001年国内生产总值达到95933亿元,比上年增长7 3%,”如果“十·五”期间(2001年~2005年)每年的国内生产总值都按此年增长率增长,那么到“十·五”末我国国内年生产总值约为_________亿元.
3%,”如果“十·五”期间(2001年~2005年)每年的国内生产总值都按此年增长率增长,那么到“十·五”末我国国内年生产总值约为_________亿元. 的定义域为
的定义域为 ,且对任意的正实数x,y有:
,且对任意的正实数x,y有: 且
且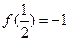 .
.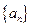 满足:
满足: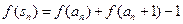 其中
其中 为数列
为数列
 成立?若存在,求出M的取值范围;若不存在,请说明理由.
成立?若存在,求出M的取值范围;若不存在,请说明理由. %,从2009年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化.
%,从2009年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化. 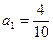 ,经过
,经过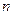 年后绿化的面积为
年后绿化的面积为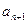 ,试用
,试用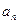 表示
表示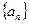 的第
的第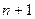 项
项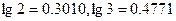 )
)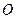 向三次曲线
向三次曲线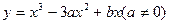 引切线,切于不同于点
引切线,切于不同于点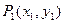 ,再由
,再由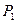 引此曲线的切线,切于不同于
引此曲线的切线,切于不同于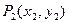 ,如此继续地作下去,……,得到点列
,如此继续地作下去,……,得到点列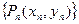 ,试回答下列问题: ⑴求
,试回答下列问题: ⑴求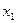 ; (2)求
; (2)求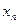 与
与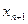 的关系式;
的关系式; 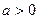 ,求证:当
,求证:当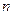 为正偶数时,
为正偶数时,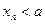 ;当
;当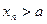 .
.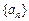 的前
的前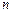 项和
项和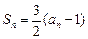 ,
,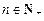 .
.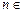 N+,集合
N+,集合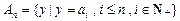 ,
,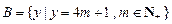 .现在集合
.现在集合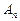 中随机取一个元素
中随机取一个元素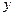 ,记
,记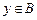 的概率为
的概率为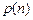 ,求
,求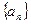 为等差数列,
为等差数列, (
(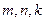 互不相等),求
互不相等),求 .
.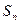 是数列
是数列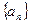 的前
的前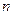 项和,
项和, 则
则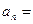 .
.