题目内容
设单调递增函数 的定义域为
的定义域为 ,且对任意的正实数x,y有:
,且对任意的正实数x,y有: 且
且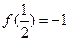 .
.
⑴.一个各项均为正数的数列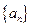 满足:
满足: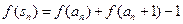 其中
其中 为数列
为数列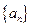 的前n项和,求数列
的前n项和,求数列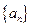 的通项公式;
的通项公式;
⑵.在⑴的条件下,是否存在正数M使下列不等式:

对一切 成立?若存在,求出M的取值范围;若不存在,请说明理由.
成立?若存在,求出M的取值范围;若不存在,请说明理由.
 的定义域为
的定义域为 ,且对任意的正实数x,y有:
,且对任意的正实数x,y有: 且
且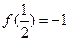 .
.⑴.一个各项均为正数的数列
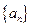 满足:
满足: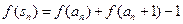 其中
其中 为数列
为数列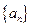 的前n项和,求数列
的前n项和,求数列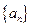 的通项公式;
的通项公式;⑵.在⑴的条件下,是否存在正数M使下列不等式:

对一切
 成立?若存在,求出M的取值范围;若不存在,请说明理由.
成立?若存在,求出M的取值范围;若不存在,请说明理由.(1)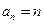 (2)
(2)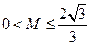
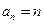 (2)
(2)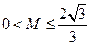
⑴、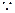 对任意的正数
对任意的正数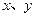 均有
均有 且
且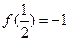 .
.
又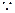
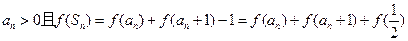
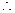
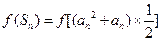 ,
,
又 是定义在
是定义在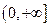 上的单增函数,
上的单增函数,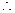
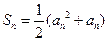 .
.
当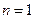 时,
时,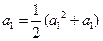 ,
,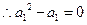 .
.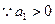 ,
,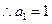 .
.
当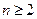 时,
时,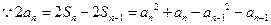 ,
,
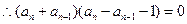 .
.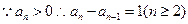 ,
,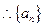 为等差数列,
为等差数列,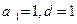 ,
,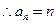 .
.
⑵、假设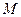 存在满足条件,
存在满足条件,
即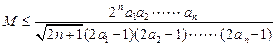 对一切
对一切 恒成立. ……………8分
恒成立. ……………8分
令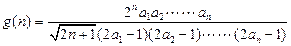 ,
,
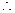
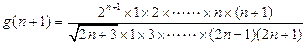 ,
,
故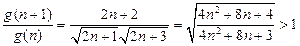 ,
,
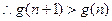 ,
,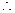
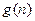 单调递增,
单调递增,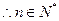 ,
,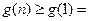
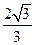 .
.
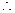
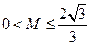 .
.

 对任意的正数
对任意的正数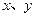 均有
均有 且
且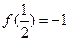 .
.又
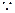
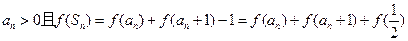
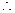
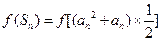 ,
, 又
 是定义在
是定义在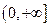 上的单增函数,
上的单增函数,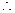
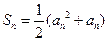 .
.当
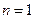 时,
时,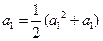 ,
,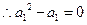 .
.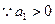 ,
,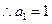 .
.当
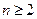 时,
时,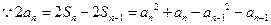 ,
,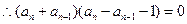 .
.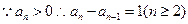 ,
,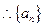 为等差数列,
为等差数列,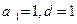 ,
,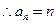 .
.⑵、假设
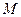 存在满足条件,
存在满足条件,即
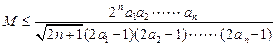 对一切
对一切 恒成立. ……………8分
恒成立. ……………8分令
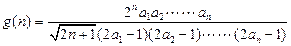 ,
,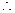
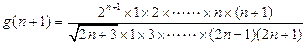 ,
, 故
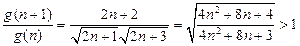 ,
,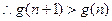 ,
,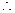
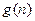 单调递增,
单调递增,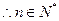 ,
,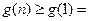
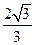 .
.
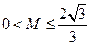 .
. 

练习册系列答案
相关题目
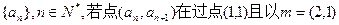 为方向向量的直线上,
为方向向量的直线上,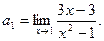 (I)求数列
(I)求数列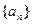 的通项公式;(II)求证:
的通项公式;(II)求证: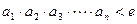 (其中e为自然对数的底数);
(其中e为自然对数的底数);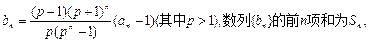
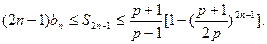
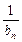 )(其中a>0且a≠1),记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1),记Sn是数列{an}的前n项和,试比较Sn与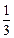 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.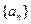 中,
中,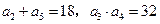 ,并且
,并且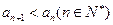 (1)求
(1)求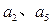 以及数列
以及数列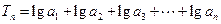 ,求当
,求当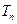 最大时
最大时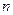 的值.
的值.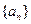 ,
,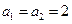 ,
,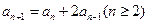
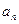
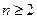 时,求证:
时,求证: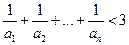
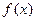 满足:
满足: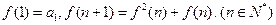
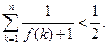
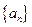 首项
首项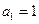 ,前
,前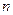 项和
项和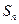 与
与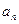 之间满足
之间满足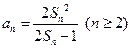
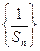 是等差数列 (2)求数列
是等差数列 (2)求数列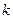 ,使
,使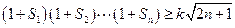 对于一切
对于一切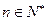 都成立,求
都成立,求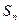 为数列
为数列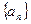 的前
的前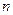 项和,
项和,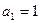 ,
,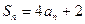 .
.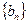 中,
中,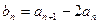 ,求证:
,求证: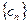 中,
中,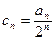 ,求证:
,求证: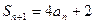 ,可利用
,可利用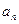 、
、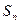 为等差数列
为等差数列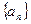 的前
的前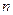 项和,
项和,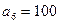 ,则
,则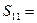 ;
;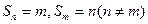 ,则
,则 .
.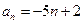 ,则其前
,则其前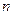 项和
项和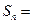 .
.