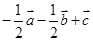题目内容
已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AD=1,AB=2,E、F分别是AB、PD的中点.
(1)求证:AF∥平面PEC;
(2)求二面角P-EC-D的大小.

(1)求证:AF∥平面PEC;
(2)求二面角P-EC-D的大小.

解法一:(1)证明:取PC的中点O,连结OF、OE.
∴FO∥DC,且FO=
DC,
∴FO∥AE.
又∵E是AB的中点,且AB=DC,
∴FO=AE.
∴四边形AEOF是平行四边形,∴AF∥OE.…(5分)
又OE?平面PEC,AF?平面PEC,
∴AF∥平面PEC.…(7分)
(2)作AM⊥CE,交CE延长线于M,连结PM.
由三垂线定理,得PM⊥CE.
∴∠PMA是二面角P-EC-D的平面角.…(11分)
由△AME~△CBE,可得AM=
.
∴tan∠PMA=
=
.
∴二面角P-EC-D的大小为arctan
.…(14分)
解法二:以A为原点,如图建立直角坐标系.则A(0,0,0),B(2,0,0),C(2,1,0),D(0,1,0),P(0,0,1),F(0,
,
),E(1,0,0),….(2分)
(1)证明:取PC的中点O,连结OE.则O(1,
,
).
=(0,
,
),
=(0,
,
),∴
∥
.…(5分)
又OE?平面PEC,AF?平面PEC,∴AF∥平面PEC.…(7分)
(2)设平面PEC的法向量为
=(x,y,z).
∵
=(1,0,-1),
=(1,1,0).
∴由
,可得
令z=-1,则
=(-1,1,-1).…(11分)
由题意可得平面ABCD的法向量是
=(0,0,-1).
∴cos<
,
>=
=
=
.
∴二面角P-EC-D的大小为arccos
.…(14分)

∴FO∥DC,且FO=
| 1 |
| 2 |
∴FO∥AE.
又∵E是AB的中点,且AB=DC,
∴FO=AE.
∴四边形AEOF是平行四边形,∴AF∥OE.…(5分)
又OE?平面PEC,AF?平面PEC,
∴AF∥平面PEC.…(7分)
(2)作AM⊥CE,交CE延长线于M,连结PM.
由三垂线定理,得PM⊥CE.
∴∠PMA是二面角P-EC-D的平面角.…(11分)
由△AME~△CBE,可得AM=
| ||
| 2 |
∴tan∠PMA=
| 1 | ||||
|
| 2 |
∴二面角P-EC-D的大小为arctan
| 2 |

解法二:以A为原点,如图建立直角坐标系.则A(0,0,0),B(2,0,0),C(2,1,0),D(0,1,0),P(0,0,1),F(0,
| 1 |
| 2 |
| 1 |
| 2 |
(1)证明:取PC的中点O,连结OE.则O(1,
| 1 |
| 2 |
| 1 |
| 2 |
| AF |
| 1 |
| 2 |
| 1 |
| 2 |
| EO |
| 1 |
| 2 |
| 1 |
| 2 |
| AF |
| EO |
又OE?平面PEC,AF?平面PEC,∴AF∥平面PEC.…(7分)
(2)设平面PEC的法向量为
| m |
∵
| PE |
| EC |
∴由
|
|
令z=-1,则
| m |
由题意可得平面ABCD的法向量是
| PA |
∴cos<
| m |
| PA |
| ||||
|
|
| 1 | ||
|
| ||
| 3 |
∴二面角P-EC-D的大小为arccos
| ||
| 3 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目





 中,
中, ,
, ,则四边形
,则四边形


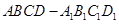 中,
中,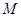 为
为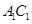 与
与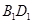 的交点。若
的交点。若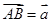 ,
,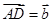 ,
,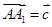 则下列向量中与
则下列向量中与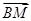 相等的向量是( )
相等的向量是( )