Question

【题目】设函数f（x）=|x+2|+|x﹣a|，x∈R
（1）若a＜0，且log2f（x）＞2对任意x∈R恒成立，求实数a的取值范围；
（2）若a＞0，且关于x的不等式f（x）＜ x有解，求实数a的取值范围．

Answer 1

【答案】
（1）解：由log2f（x）＞2对任意x∈R恒成立，得f（x）＞4对任意x∈R恒成立，

即|x+2|+|x﹣a|＞4对任意x∈R恒成立，

也就是（|x+2|+|x﹣a|）min＞4对任意x∈R恒成立，

由|x+2|+|x﹣a|≥|（x+2）﹣（x﹣a）|=|2+a|，

得|2+a|＞4，即2+a＜﹣4或2+a＞4，解得a＜﹣6或a＞2，

∵a＜0，∴a＜﹣6

（2）解：∵a＞0，

∴f（x）=|x+2|+|x﹣a|= ，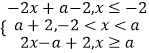

画出函数y=f（x）与y= 的图象如图，

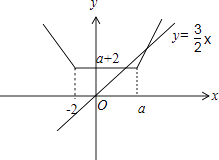
由图可知，要使关于x的不等式f（x）＜ x有解，则 ，解得a＞4

【解析】（1）利用绝对值的不等式求得f（x）=|x+2|+|x﹣a|的最小值，再由最小值大于4求得a的范围；（2）写出分段函数解析式，画出图形，数形结合列式求解．