题目内容
17.数列{cn}为等比数列,其中c1=2,c8=4,f(x)=x(x-c1)(x-c2)…(x-c8),f′(x)为函数f(x)的导函数,则f′(0)=( )| A. | 0 | B. | 26 | C. | 29 | D. | 212 |
分析 由已知求出数列{cn}的通项公式,对函数f(x)求导,求出f′(x),令x=0求值.
解答 解:因为数列{cn}为等比数列,其中c1=2,c8=4,
所以公比q=${2}^{\frac{1}{7}}$,
由f(x)=x(x-c1)(x-c2)…(x-c8),得f′(x)=(x-c1)(x-c2)…(x-c8)+x[(x-c1)(x-c2)…(x-c8)]',
所以f′(0)=(-c1)(-c2)…(-c8)=c1c2…c8=${2}^{1+\frac{8}{7}+\frac{9}{7}…+2}$=212;
故选D.
点评 本题考查了等比数列的通项求法以及导数的运算;解答本题求出等比数列的通项公式以及函数的导数是关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
12.在等差数列{an}中,已知a2=3,公差d=2,设bn=$\frac{2}{{a}_{n}{a}_{n+1}}$,则数列{bn}的前n项和Tn=( )
| A. | $\frac{1}{2n+1}$ | B. | $\frac{2n+2}{2n+1}$ | C. | $\frac{2n}{2n+1}$ | D. | $\frac{n}{2n+1}$ |
7.若直线l:ax-by=1与不等式组$\left\{\begin{array}{l}y<1\\ 3x-y-2<0\\ 3x+y+2>0\end{array}\right.$表示的平面区域无公共点,则3a-2b的最小值为( )
| A. | $\frac{7}{2}$ | B. | $-\frac{11}{2}$ | C. | 2 | D. | -2 |
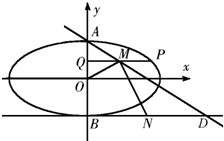 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.