题目内容
18.已知sinα+cosα=$\frac{1}{5}$,α∈(0,π),求sinα-cosα及tanα的值.分析 把已知等式两边平方,利用完全平方公式及同角三角函数间的基本关系变形求出2sinαcosα的值,进而判断出sinα-cosα的正负,利用完全平方公式及同角三角函数间的基本关系求出sinα-cosα的值,联立求出sinα与cosα的值,即可确定出tanα的值.
解答 解:把sinα+cosα=$\frac{1}{5}$①,两边平方得:(sinα+cosα)2=1+2sinαcosα=$\frac{1}{25}$,
∴2sinαcosα=-$\frac{24}{25}$,
∵α∈(0,π),
∴sinα>0,cosα<0,即sinα-cosα>0,
∴(sinα-cosα)2=1-2sinαcosα=$\frac{49}{25}$,即sinα-cosα=$\frac{7}{5}$②,
联立①②,解得:sinα=$\frac{4}{5}$,cosα=-$\frac{3}{5}$,
则tanα=-$\frac{4}{3}$.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.在边长为1的正三角形ABC中,|$\overrightarrow{AB}$-$\overrightarrow{BC}$|的值为( )
| A. | 1 | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
12.在等差数列{an}中,已知a2=3,公差d=2,设bn=$\frac{2}{{a}_{n}{a}_{n+1}}$,则数列{bn}的前n项和Tn=( )
| A. | $\frac{1}{2n+1}$ | B. | $\frac{2n+2}{2n+1}$ | C. | $\frac{2n}{2n+1}$ | D. | $\frac{n}{2n+1}$ |
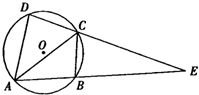 如图所示,四边形ABCD的外接圆为圆O,线段AB与线段DC的延长线交于点E,$\frac{AD}{DE}$=$\frac{1}{3}$.
如图所示,四边形ABCD的外接圆为圆O,线段AB与线段DC的延长线交于点E,$\frac{AD}{DE}$=$\frac{1}{3}$.