题目内容
一颗骰子连续掷两次,朝上的点数依次为 、
、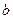 ,使复数
,使复数 为实数的概率是 ( )
为实数的概率是 ( )
 、
、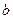 ,使复数
,使复数 为实数的概率是 ( )
为实数的概率是 ( )A. | B. | C. | D. |
D
本题是一个古典概型,试验发生包含的事件是一颗骰子连续掷两次,共有6×6种结果,满足条件的事件是使复数(a+bi)(b-4ai)为实数,进行复数的乘法运算,得到b=2a的结果,列举出所有情况,得到概率.
解:由题意知本题是一个古典概型,
试验发生包含的事件是一颗骰子连续掷两次,共有6×6=36种结果,
满足条件的事件是使复数(a+bi)(b-4ai)为实数,
∵(a+bi)(b-4ai)=5ab-(4a2-b2)i,
要使的这是一个实数,
有4a2-b2=0,
∴4a2=b2,
∴b=2a,
有a=1,b=2;a=2,b=4;a=3,b=6,共有3种结果,
∴由古典概型得到P=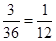 ,
,
故选D.
解:由题意知本题是一个古典概型,
试验发生包含的事件是一颗骰子连续掷两次,共有6×6=36种结果,
满足条件的事件是使复数(a+bi)(b-4ai)为实数,
∵(a+bi)(b-4ai)=5ab-(4a2-b2)i,
要使的这是一个实数,
有4a2-b2=0,
∴4a2=b2,
∴b=2a,
有a=1,b=2;a=2,b=4;a=3,b=6,共有3种结果,
∴由古典概型得到P=
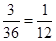 ,
,故选D.

练习册系列答案
相关题目
 为这五名专家到A校评估的人数,求
为这五名专家到A校评估的人数,求



 分)袋中有质地、大小完全相同的
分)袋中有质地、大小完全相同的 个球,编号分别为
个球,编号分别为 、
、 、
、 、
、 、
、 的正方体
的正方体 内任取一点
内任取一点 ,则点
,则点 的距离小于或等于
的距离小于或等于 )
)  ,
, ,移栽后成活的概率分别为
,移栽后成活的概率分别为 ,
, .
. )分别为
)分别为 ,
, ,
,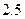 ,
, ,若从中一次随机抽取
,若从中一次随机抽取 根
根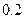
 {1,2,3,4},若|a
{1,2,3,4},若|a b|
b|  1,则称甲乙”心有灵犀”.现任意找两个人玩这个游戏,得出他们”心有灵犀”的概率为 (分式表示)
1,则称甲乙”心有灵犀”.现任意找两个人玩这个游戏,得出他们”心有灵犀”的概率为 (分式表示)