题目内容
(本小题满分12分)四川灾后重建工程督导评估小组五名专家被随机分配到A、B、C、D四所不同的学校进行重建评估工作,要求每所学校至少有一名专家。
(1)求评估小组中甲、乙两名专家同时被分配到A校的概率;
(2)求评估小组中甲、乙两名专家不在同一所学校的概率;
(3)设随机变量 为这五名专家到A校评估的人数,求
为这五名专家到A校评估的人数,求 的数学期望E
的数学期望E 。
。
(1)求评估小组中甲、乙两名专家同时被分配到A校的概率;
(2)求评估小组中甲、乙两名专家不在同一所学校的概率;
(3)设随机变量
 为这五名专家到A校评估的人数,求
为这五名专家到A校评估的人数,求 的数学期望E
的数学期望E 。
。解:(1)记评估小组中甲、乙两名专家同时被分配到A校的事件为E,则P(E)= ,所以评估小组中甲、乙两名专家同时被分配到A校的概率为
,所以评估小组中甲、乙两名专家同时被分配到A校的概率为 。
。
(2)记评估小组中甲、乙两名专家被分配在同一所学校的事件为F,那么P(F)= ,所以甲、乙两名专家不在同一所学校的概率为:P(
,所以甲、乙两名专家不在同一所学校的概率为:P( )=1-P(F)=
)=1-P(F)=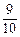 。
。
(3)随机变量 的可能取值为1,2,则P(
的可能取值为1,2,则P( ="2)="
="2)=" 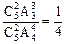 ;P(
;P( =1)=1-P(
=1)=1-P( =2)=
=2)= 。
。
所以 的分布列是:
的分布列是:
所以 的数学期望E
的数学期望E =1×
=1× +2×
+2× =
= 。
。
 ,所以评估小组中甲、乙两名专家同时被分配到A校的概率为
,所以评估小组中甲、乙两名专家同时被分配到A校的概率为 。
。(2)记评估小组中甲、乙两名专家被分配在同一所学校的事件为F,那么P(F)=
 ,所以甲、乙两名专家不在同一所学校的概率为:P(
,所以甲、乙两名专家不在同一所学校的概率为:P( )=1-P(F)=
)=1-P(F)=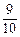 。
。(3)随机变量
 的可能取值为1,2,则P(
的可能取值为1,2,则P( ="2)="
="2)=" 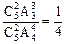 ;P(
;P( =1)=1-P(
=1)=1-P( =2)=
=2)= 。
。所以
 的分布列是:
的分布列是: | 1 | 2 |
| P |  |  |
 的数学期望E
的数学期望E =1×
=1× +2×
+2× =
= 。
。略

练习册系列答案
相关题目
 小题满分12分)
小题满分12分) F三家企业来自河南省,此项工程需要两家企业联合施工,假设每家企业中标的概率相同.
F三家企业来自河南省,此项工程需要两家企业联合施工,假设每家企业中标的概率相同. 少有一家来自山东省的概率是多少?
少有一家来自山东省的概率是多少? ,乙获胜的概率是
,乙获胜的概率是 ,则
,则 是( )
是( ) 、
、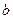 ,使复数
,使复数 为实数的概率是 ( )
为实数的概率是 ( )



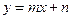 .设集合
.设集合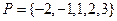 和
和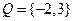 ,分别从集合
,分别从集合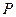 和
和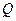 中随机取一个数作为
中随机取一个数作为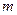 和
和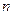 ,则函数
,则函数 的分布列与均值。
的分布列与均值。 满足
满足 ,则关于
,则关于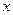 的方程
的方程 有实数根的概率是
有实数根的概率是



 ,过坐标原点和点P(
,过坐标原点和点P( ,求
,求 的概率;
的概率; ,且
,且 ,过坐标原点和点P(
,过坐标原点和点P(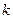 ,求
,求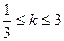 的概率。
的概率。