Question

选修4-1：几何证明选讲
如图，AB为圆O的直径，CD为垂直于AB的一条弦，垂足为E，弦BM与CD交于点F．
（Ⅰ）证明：A、E、F、M四点共圆；
（Ⅱ）证明：AC²+BF•BM=AB²．

Answer 1

证明：（I）如图所示．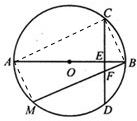
连接AM，∵AB是⊙O的直径，∴∠AMB=90°．
∴∠AMB+∠AEF=180°，
∴A、E、F、M四点共圆；
（II）连接AC，BC．
由A、E、F、M四点共圆，∴BF•BM=BE•BA．
连接AC，BC．则∠ACB=90°．
又CD⊥AB．
∴AC²=AE•AB．
∴AC²+BF•BM=AE•AB+BE•AB=AB²．