题目内容
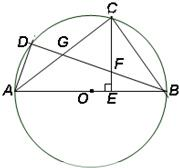
如图，四边形ABCD内接于⊙O，
=
，过A点的切线交CB的延长线于E点．求证：AB2=BE•CD．
 |
| AB |
|
| AD |
证明：连接AC，
∵EA切⊙O于A，
∴∠EAB=∠ACB．
∵
=
，
∴∠ACD=∠ACB，AB=AD．
于是∠EAB=∠ACD．
又四边形ABCD内接于⊙O，
∴∠ABE=∠D．
∴△ABE∽△CDA．
于是
=
，即AB•DA=BE•CD．
∴AB2=BE•CD．
∵EA切⊙O于A，
∴∠EAB=∠ACB．
∵
|
| AB |
|
| AD |
∴∠ACD=∠ACB，AB=AD．
于是∠EAB=∠ACD．
又四边形ABCD内接于⊙O，
∴∠ABE=∠D．
∴△ABE∽△CDA．
于是
| AB |
| CD |
| BE |
| DA |
∴AB2=BE•CD．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
中，
，
是
边上的高，
是
重合），
，
，垂足分别为
．
；
与
是否垂直？若垂直，请给出证明；若不垂直，请说明理由；
时，
为等腰直角三角形吗？并说明理由．
