题目内容
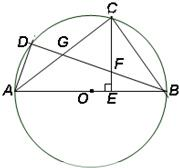
如图，AC是⊙O的直径，∠ACB=60°，连接AB，分别过A、B作圆O的切线，两切线交于点P，若已知⊙O的半径为1，求△PAB的周长．
∵PA，PB是圆O的切线．
∴PA=PB，∠PAB=60°
∴△PAB是等边三角形．
在直角△ABC中，AB=AC•sin60°=2×
=
∴PA=PB=AB=3
．
∴PA=PB，∠PAB=60°
∴△PAB是等边三角形．
在直角△ABC中，AB=AC•sin60°=2×
| ||
| 2 |
| 3 |
∴PA=PB=AB=3
| 3 |
练习册系列答案
相关题目
