题目内容
【题目】如图,长方体![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
, ![]() 的中点,过点
的中点,过点![]() 的平面
的平面![]() 与平面
与平面![]() 平行,且与长方体的面相交,交线围成一个几何图形.
平行,且与长方体的面相交,交线围成一个几何图形.
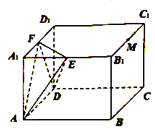
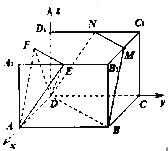
(1)在图中画出这个几何图形(说明画法,不需要说明理由);
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)利用平行关系作图;(2)建立空间直角坐标系,求出两个法向量, ![]() ,
, ![]() ,求出二面角。
,求出二面角。
试题解析:
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,
, ![]() ,则交线围成的几何图形
,则交线围成的几何图形![]() 如图:
如图:
(2)因为点![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,
的中点, ![]() ,
,
所以![]() ,
, ![]()
以![]() 为坐标原点,
为坐标原点, ![]() 的方向为
的方向为![]() 轴的正方向,建立如图所示空间直角坐标系
轴的正方向,建立如图所示空间直角坐标系![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
设![]() 是平面
是平面![]() 的法向量,则
的法向量,则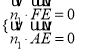 ,即
,即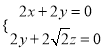
所以可取![]() .
.
同理可求平面![]() 的一个法向量为
的一个法向量为![]()
因为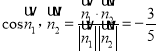
所以二面角![]() 的余弦值为
的余弦值为![]()
试题分析:本题考查立体几何的二面角求解。一般的,在容易建系的立体几何问题中,采取空间直角坐标系解题比较方便,可以避免找角或其他技巧性方法,将几何问题转化为代数计算,只需掌握解题套路,即可解决问题。

练习册系列答案
相关题目
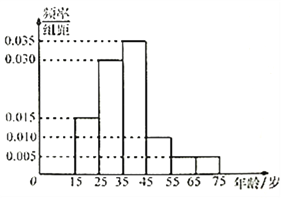
【题目】2017年5月14日,第一届“一带一路”国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在![]() 岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为:
岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为: ![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .把年龄落在区间
.把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年”和“中老年”.
内的人分别称为“青少年”和“中老年”.
(1)根据频率分布直方图求样本的中位数(保留两位小数)和众数
(2)根据已知条件完成下面的2×2列联表,并判断能否有99%的把握认为关注“带一路”是否和年龄段有关?
关注 | 不关注 | 合计 | |
青少年 | 15 | ||
中老年 | |||
合计 | 50 | 50 | 100 |
附:参考公式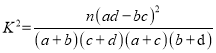 ,其中
,其中![]()
临界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |