题目内容
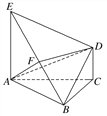
【题目】如图，四棱锥P－ABCD的底面为矩形，AB＝
，BC＝1，E，F分别是AB，PC的中点，DE⊥PA.
(1)求证：EF∥平面PAD；
(2)求证：平面PAC⊥平面PDE.
【答案】(1)见解析；(2)见解析.
【解析】试题分析：（1）取PD中点G，根据平几知识可得AEFG为平行四边形，即得EF∥AG，再根据线面平行判定定理得结论（2）由矩形性质得DE⊥AC.又DE⊥PA.因此由线面垂直判定定理得DE⊥平面PAC.再根据面面垂直判定定理得结论
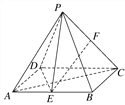
试题解析：证明 (1)如图，取PD中点G，连接AG，FG，
因为F，G分别为PC，PD的中点，所以FG∥CD，且FG＝
CD.
又因为E为AB中点，所以AE∥CD，且AE＝CD.
所以AE∥FG，AE＝FG.
所以四边形AEFG为平行四边形．
所以EF∥AG，又EF平面PAD，
AG平面PAD，
所以EF∥平面PAD.
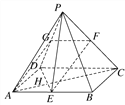
(2)设AC∩DE＝H，由△AEH∽△CDH及E为AB中点，得
＝
＝，
又因为AB＝
，BC＝1，
所以AC＝
，AH＝
AC＝
.
所以
＝
＝
，又∠BAC为公共角，所以△HAE∽△BAC.
所以∠AHE＝∠ABC＝90°，
即DE⊥AC.
又DE⊥PA，PA∩AC＝A，PA平面PAC，AC平面PAC，所以DE⊥平面PAC.
又DE平面PDE，
所以平面PAC⊥平面PDE.
练习册系列答案
名校课堂系列答案
相关题目
