题目内容
以椭圆上一点和两个焦点为顶点的三角形的最大面积为1,则长轴长的最小值为

本试题主要是考查了运用三角形的面积公式得到bc的值,然后结合a2=b2+c2,求解2a的最值。
由题意可知,因为椭圆上一点和两个焦点为顶点的三角形的最大面积为1,即可知bc=1,因为a2=b2+c2=b2+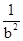
 ,那么运用均值不等式,所以a
,那么运用均值不等式,所以a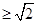 故长轴长的最小值为
故长轴长的最小值为 ,答案为
,答案为 。
。
解决该试题的关键是利用均值不等式得到最值。
由题意可知,因为椭圆上一点和两个焦点为顶点的三角形的最大面积为1,即可知bc=1,因为a2=b2+c2=b2+
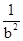
 ,那么运用均值不等式,所以a
,那么运用均值不等式,所以a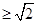 故长轴长的最小值为
故长轴长的最小值为 ,答案为
,答案为 。
。解决该试题的关键是利用均值不等式得到最值。

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
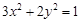 的焦点坐标是( )
的焦点坐标是( ) )、(0,
)、(0, )
) 的左右焦点分别为
的左右焦点分别为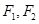 ,过焦点
,过焦点 的直线交该椭圆于
的直线交该椭圆于 两点,若
两点,若 的内切圆面积为
的内切圆面积为 ,
, ,则
,则 的值为 。
的值为 。 被椭圆
被椭圆 所截得的弦的中点坐标是( )
所截得的弦的中点坐标是( ) ,
, 
 ,
,  ,
,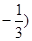
 ,
, 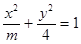 ,对于任意实数
,对于任意实数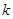 下列直线被椭圆E截得的弦长与直线
下列直线被椭圆E截得的弦长与直线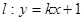 被椭圆E截得的弦长不可能相等的是( )
被椭圆E截得的弦长不可能相等的是( )

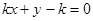

 中,椭圆
中,椭圆 为
为
 ,且线段
,且线段 恰以点
恰以点 为中点,求直线
为中点,求直线 的直线
的直线 (非
(非 轴)与椭圆
轴)与椭圆 试问在
试问在 ,使
,使 恒为定值
恒为定值 ?若存在,求出点
?若存在,求出点 的坐标及实数
的坐标及实数
 经过点
经过点 ,一个焦点是
,一个焦点是 .
. 的方程;
的方程; 轴的两个交点为
轴的两个交点为 、
、 ,点
,点 在直线
在直线 上,直线
上,直线 、
、 分别与椭圆
分别与椭圆 、
、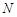 两点.试问:当点
两点.试问:当点 是否恒经过定点
是否恒经过定点 ?证明你的结论.
?证明你的结论.