题目内容
设 ∈(0,
∈(0, ),方程
),方程 表示焦点在x轴上的椭圆,则
表示焦点在x轴上的椭圆,则 ∈( )
∈( )
 ∈(0,
∈(0, ),方程
),方程 表示焦点在x轴上的椭圆,则
表示焦点在x轴上的椭圆,则 ∈( )
∈( )A.(0,  | B.( , ,  ) ) | C.(0, ) ) | D.[ , , ) ) |
B
解:因为设 ∈(0,
∈(0, ),方程
),方程 表示焦点在x轴上的椭圆,则
表示焦点在x轴上的椭圆,则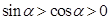 ,因此
,因此 ∈((
∈(( ,
,  ) ,选B
) ,选B
 ∈(0,
∈(0, ),方程
),方程 表示焦点在x轴上的椭圆,则
表示焦点在x轴上的椭圆,则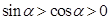 ,因此
,因此 ∈((
∈(( ,
,  ) ,选B
) ,选B
练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 被椭圆
被椭圆 所截得的弦的中点坐标是( )
所截得的弦的中点坐标是( ) ,
, 
 ,
,  ,
,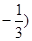
 ,
,  的左、右顶点分别A、B,椭圆过点(0,1)且离心率
的左、右顶点分别A、B,椭圆过点(0,1)且离心率 .
. 轴,H为垂足,延长HP到点Q,且PQ=HP,过点B作直线
轴,H为垂足,延长HP到点Q,且PQ=HP,过点B作直线 轴,连结AQ并延长交直线
轴,连结AQ并延长交直线 于点M,N为MB的中点,试判断直线QN与以AB为直径的圆O的位置关系.
于点M,N为MB的中点,试判断直线QN与以AB为直径的圆O的位置关系.
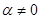 的直线
的直线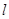 过椭圆
过椭圆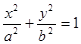
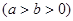 的右焦点F交椭圆于A、B两点,P为右准线上任意一点,则
的右焦点F交椭圆于A、B两点,P为右准线上任意一点,则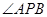 为 ( )
为 ( )
 中,
中, ,动点P的轨迹为曲线E,曲线E过点C且满足|PA|+|PB|为常数。
,动点P的轨迹为曲线E,曲线E过点C且满足|PA|+|PB|为常数。 平分?若存在,求出L的斜率的取值范围;若不存在说明理由。
平分?若存在,求出L的斜率的取值范围;若不存在说明理由。 轴上,经过点
轴上,经过点 ,离心率
,离心率 .
.
 、
、 ,点
,点 为直线
为直线 上任意一点(点
上任意一点(点 交椭圆于
交椭圆于 点,连结
点,连结 并延长交椭圆于
并延长交椭圆于 点,试问:是否存在
点,试问:是否存在 ,使得
,使得 成立,若存在,求出
成立,若存在,求出 上一点P到焦点F1的距离为7,则点P到F2相对应的准线的距离是____;
上一点P到焦点F1的距离为7,则点P到F2相对应的准线的距离是____;