题目内容
已知数列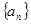 中,
中,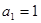 ,
,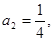 且
且
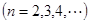 .
.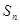 为数列
为数列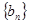 的前
的前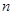 项和,且
项和,且
 .
.
(1)求数列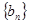 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列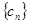 的前
的前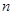 项的和
项的和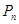 ;
;
(3)证明对一切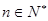 ,有
,有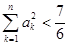 .
.
(1)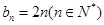 ;(2)
;(2)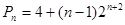 ;(3)证明过程详见解析.
;(3)证明过程详见解析.
解析试题分析:本题主要考查数列的通项公式、递推公式、裂项相消法、数学归纳法、错位相减法等基础知识,考查学生分析问题解决问题的能力,转化能力和计算能力.第一问,用n-1代替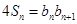 中的n,得到一个等式,2个等式相减,得到
中的n,得到一个等式,2个等式相减,得到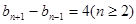 ,分n为奇数偶数进行讨论,分别求出
,分n为奇数偶数进行讨论,分别求出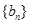 的通项公式,由于得到的式子相同,所以
的通项公式,由于得到的式子相同,所以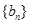 的通项公式就是
的通项公式就是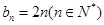 ;第二问,要求数列
;第二问,要求数列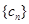 的前n项和,关键是需要求出
的前n项和,关键是需要求出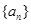 的通项公式,可以利用已知的递推公式进行推导,也可以利用数学归纳法猜想证明,得到
的通项公式,可以利用已知的递推公式进行推导,也可以利用数学归纳法猜想证明,得到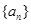 的通项公式后,代入到
的通项公式后,代入到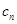 中,得到
中,得到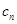 的通项公式,最后用错位相减法进行求和;第三问,先用放缩法对原式进行变形,再用裂项相消法求和,最后和
的通项公式,最后用错位相减法进行求和;第三问,先用放缩法对原式进行变形,再用裂项相消法求和,最后和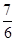 作比较.
作比较.
试题解析:(1)由已知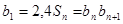 得
得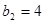 ,
,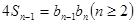 ,
,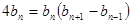 ,
,
由题意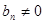 ,即
,即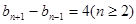 ,当n为奇数时,
,当n为奇数时,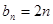 ;当n为偶数时,
;当n为偶数时,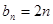 .
.
所以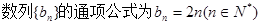 .4分
.4分
(2)解法一:由已知,对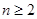 有
有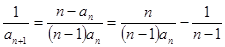 ,
,
两边同除以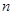 ,得
,得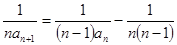 ,即
,即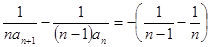 ,
,
于是,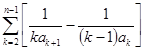 =
=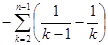 =
=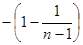 ,
,
即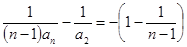 ,
,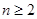 ,所以
,所以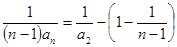 =
=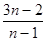 ,
,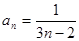 ,
,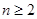 ,又
,又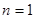 时也成立,故
时也成立,故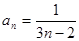 ,
,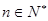 .
.
所以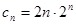 ,
,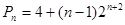 8分
8分
解法二:也可以归纳、猜想得出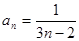 ,然后用数学归纳法证明.
,然后用数学归纳法证明.
(3)当 ,有
,有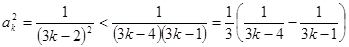 ,
,
所以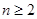 时,有
时,有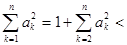
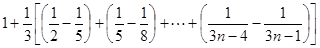
=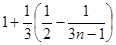
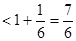 .
.
当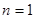 时,
时,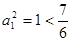 .故对一切
.故对一切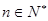 ,有
,有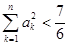 .14分
.14分
考点:1.由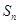 求
求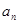 ;2.错位相减法;3.数学归纳法;4.裂项相消法.
;2.错位相减法;3.数学归纳法;4.裂项相消法.

练习册系列答案
相关题目
 的首项
的首项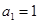 ,前
,前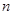 项和为
项和为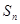 ,且
,且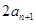 ,
,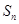 ,
,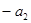 成等差数列,其中
成等差数列,其中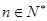 .
.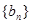 满足:
满足: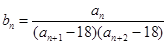 ,记数列
,记数列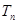 ,求
,求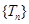 的最大项.
的最大项.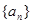 的首项
的首项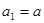 ,
,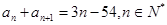
 项和为
项和为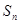 ,若
,若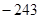 ,求
,求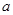 的取值范围?
的取值范围?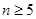 ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如: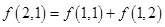 ;
;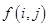 为数表中第
为数表中第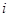 行的第
行的第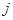 个数.
个数.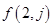 和
和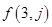 ;
;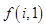 关于
关于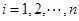 )的表达式.
)的表达式.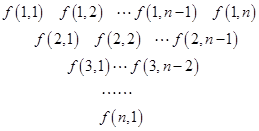
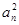 ·bn,证明:当且仅当n≥3时,cn+1<cn..
·bn,证明:当且仅当n≥3时,cn+1<cn.. 的前
的前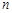 项和为
项和为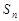 ,首项
,首项 ,点
,点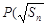 ,
,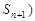 在曲线
在曲线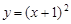 上.
上.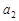 ,
,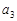 ;
;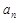 ;
;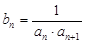 ,
,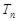 表示数列
表示数列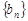 的前项和,若
的前项和,若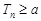 恒成立,求
恒成立,求 的取值范围.
的取值范围.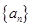 的前
的前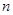 项和为
项和为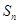 ,
,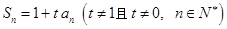 .
. ,求实数
,求实数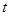 的取值范围.
的取值范围. ,
,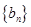 满足
满足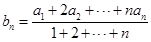
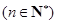 .
.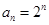 ,求数列
,求数列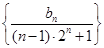 的前
的前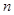 项和
项和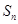 .
.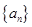 满足递推式:
满足递推式: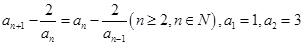 .
.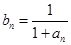 ,求
,求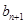 与
与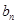 的递推关系(用
的递推关系(用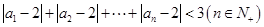 .
.